1  ¿Por qué estadística?

Notas

Adaptado casi al pie de la letra de los capítulos 1 y 2 de Navarro, D. J. “Learning Statistics with R.” https://compcogscisydney.org/learning-statistics-with-r/. Traducido al español rioplatense por ChatGPT4-o bajo la supervisión de Álvaro Cabana.

Consultar al estadístico después de que un experimento ha terminado es, a menudo, simplemente pedirle que realice una autopsia. Tal vez pueda decir de qué murió el experimento. — Sir Ronald Fisher

1.1 Sobre la psicología de la estadística

Para sorpresa de muchos estudiantes, la estadística es una parte bastante importante de la formación en psicología. Para sorpresa de nadie, la estadística rara vez es la parte favorita de esa formación. Después de todo, si realmente te encantara la idea de hacer estadística, probablemente estarías en una clase de estadística ahora mismo, no en una clase de psicología. Así que, como era de esperar, hay una buena parte del estudiantado que no está muy feliz con el hecho de que la psicología incluya tanta estadística. Por eso, me pareció un buen punto de partida responder algunas de las preguntas más comunes que suelen tener sobre este tema…

Una parte importante del problema tiene que ver con la idea misma de estadística. ¿Qué es? ¿Para qué sirve? ¿Y por qué los científicos están tan obsesionados con ella? Son todas buenas preguntas. Empecemos por la última. Como grupo, los científicos parecen estar extrañamente empeñados en hacer pruebas estadísticas de todo. De hecho, usamos estadísticas tan seguido que a veces se nos olvida explicar por qué lo hacemos. Es casi un dogma entre los científicos —y especialmente entre los de las ciencias sociales— que los resultados no son confiables hasta que hacemos estadística. A los estudiantes de grado se les podría perdonar por pensar que estamos completamente locos, porque nadie se toma el tiempo de responder una pregunta muy simple:

¿Por qué hacen estadística? ¿Por qué no usar solo el sentido común?

Es una pregunta ingenua en cierto sentido, pero muchas de las buenas preguntas lo son. Hay muchas buenas respuestas, pero para mí, la mejor es muy simple: no confiamos lo suficiente en nosotros mismos. Nos preocupa ser humanos, y estar sujetos a todos los sesgos, tentaciones y debilidades que eso implica. Gran parte de la estadística funciona como una especie de red de seguridad. Usar el “sentido común” para evaluar evidencia implica confiar en las corazonadas, en los argumentos verbales y en el puro poder del razonamiento humano para llegar a la respuesta correcta. La mayoría de los científicos no cree que ese enfoque funcione muy bien.

De hecho, pensándolo bien, esto suena bastante a una pregunta psicológica. Y como trabajo en un departamento de psicología, parece buena idea profundizar un poco más. ¿Es realmente razonable pensar que el “sentido común” es confiable? Los argumentos verbales tienen que construirse con lenguaje, y todo lenguaje tiene sesgos: algunas cosas son más difíciles de decir que otras, y no necesariamente porque sean falsas (por ejemplo, la electrodinámica cuántica es una buena teoría, pero difícil de explicar con palabras). Las corazonadas no están diseñadas para resolver problemas científicos, sino para manejar inferencias cotidianas —y considerando que la evolución biológica es más lenta que el cambio cultural, deberíamos decir que están diseñadas para resolver problemas de otro mundo, distinto al que vivimos ahora. Más fundamentalmente, razonar con sentido común requiere hacer “inducción”, es decir, conjeturas razonables y generalizaciones más allá de la evidencia inmediata. Si creés que podés hacer eso sin verte influenciado por distracciones o sesgos, bueno… te puedo vender el obelisco. De hecho, como veremos en la siguiente sección, ni siquiera podemos resolver problemas deductivos (que no requieren conjeturas) sin que nuestros sesgos previos se metan en el medio.

1.1.1 La maldición del sesgo de creencia

La mayoría de las personas son bastante inteligentes. Claramente más que otras especies con las que compartimos el planeta (aunque muchos no estarían de acuerdo). Nuestras mentes son asombrosas, capaces de hazañas increíbles de pensamiento y razonamiento. Pero eso no nos hace perfectos. Una de las muchas cosas que la psicología ha demostrado a lo largo del tiempo es que nos cuesta mucho mantenernos neutrales, evaluar la evidencia de manera imparcial y sin dejarnos llevar por nuestras creencias previas. Un buen ejemplo de esto es el sesgo de creencia en el razonamiento lógico: si le pedís a alguien que juzgue si un argumento es lógicamente válido (es decir, si la conclusión se sigue de las premisas), solemos dejarnos influenciar por qué tan creíble parece la conclusión, incluso cuando no deberíamos. Por ejemplo, este argumento es válido y tiene una conclusión creíble:

• Ningún cigarrillo es barato (Premisa 1)
• Algunas cosas adictivas son baratas (Premisa 2)
• Por lo tanto, algunas cosas adictivas no son cigarrillos (Conclusión)

Y este también es válido, pero la conclusión suena menos creíble:

• Ninguna cosa adictiva es barata (Premisa 1)
• Algunos cigarrillos son baratos (Premisa 2)
• Por lo tanto, algunos cigarrillos no son adictivos (Conclusión)

La estructura lógica del argumento #2 es idéntica a la del #1, y ambos son válidos. Sin embargo, en el segundo caso, hay buenas razones para pensar que la premisa 1 es falsa, así que probablemente también lo sea la conclusión. Pero eso no importa: un argumento es deductivamente válido si la conclusión se sigue lógicamente de las premisas. No importa si las premisas o la conclusión son verdaderas. Ahora veamos un argumento inválido con una conclusión creíble:

• Ninguna cosa adictiva es barata (Premisa 1)
• Algunos cigarrillos son baratos (Premisa 2)
• Por lo tanto, algunas cosas adictivas no son cigarrillos (Conclusión)

Y uno inválido con una conclusión poco creíble:

• Ningún cigarrillo es barato (Premisa 1)
• Algunas cosas adictivas son baratas (Premisa 2)
• Por lo tanto, algunos cigarrillos no son adictivos (Conclusión)

Ahora bien, supongamos que las personas realmente pueden dejar de lado sus sesgos previos sobre qué es verdadero y qué no, y evaluar un argumento únicamente por su lógica. Esperaríamos que el 100% diga que los argumentos válidos son válidos, y que el 0% diga que los inválidos lo son. Si hiciéramos un experimento sobre esto, esperaríamos ver datos así:

	la conclusión parece verdadera	la conclusión parece falsa
el argumento es válido	100% dice “válido”	100% dice “válido”
el argumento es inválido	0% dice “válido”	0% dice “válido”

Si los datos psicológicos se vieran así (o incluso se acercaran bastante), podríamos sentirnos seguros confiando en nuestras corazonadas. O sea, estaría perfecto dejar que los científicos evaluaran los datos según su sentido común, sin molestarse con todo este asunto turbio de la estadística. Pero ustedes ya han cursado psicología, y a esta altura seguro sospechan hacia dónde va esto.

En un estudio clásico, Evans, Barston, y Pollard (1983) hicieron un experimento sobre esto mismo. Y lo que encontraron fue que, cuando las creencias previas (o sea, los sesgos) coincidían con la estructura lógica del argumento, todo iba bastante bien:

	la conclusión parece verdadera	la conclusión parece falsa
el argumento es válido	92% dice “válido”	–
el argumento es inválido	–	8% dice “válido”

No es perfecto, pero está bastante bien. Ahora mirá lo que pasa cuando la intuición sobre la verdad de la conclusión entra en conflicto con la lógica del argumento:

	la conclusión parece verdadera	la conclusión parece falsa
el argumento es válido	92% dice “válido”	46% dice “válido”
el argumento es inválido	92% dice “válido”	8% dice “válido”

Ay. Eso ya no está tan bien. Al parecer, cuando a la gente se le presenta un argumento fuerte que contradice sus creencias previas, le cuesta bastante incluso reconocer que es un buen argumento (solo el 46% lo logró). Y peor todavía: cuando se les da un argumento débil que coincide con sus creencias, casi nadie nota que es débil (¡el 92% se equivocó!).

Ahora bien, si lo pensás, tampoco es que estos datos sean una catástrofe total. En promedio, a la gente le va un poco mejor que al azar al tratar de compensar sus sesgos previos: más o menos el 60% de los juicios fueron correctos (el azar daría 50%). Aun así, si fueras un profesional encargado de evaluar evidencia, y alguien te ofreciera una herramienta mágica que mejora tus chances de decidir bien del 60% al 95%, ¿no la aceptarías? Obvio que sí. Por suerte, esa herramienta existe. No es magia, es estadística. Y esa es la razón #1 por la que los científicos aman la estadística: es demasiado fácil creer lo que una ya cree; así que si queremos “creer en los datos” en lugar de nuestras intuiciones, necesitamos una ayudita para mantener a raya nuestros sesgos. Eso es lo que hace la estadística: nos ayuda a ser honestos.

1.2 La advertencia de la paradoja de Simpson

La siguiente es una historia real (creo…). En 1973, la Universidad de California en Berkeley estaba preocupada por los ingresos a sus programas de posgrado. En particular, el problema era la distribución por género de los ingresos, que se veía así:

	Número de postulantes	Percentaje admitido
Hombres	8442	44%
Mujeres	4321	35%

Y tenían miedo de que los demandaran. Con casi 13.000 postulantes, una diferencia del 9% entre hombres y mujeres es demasiado grande como para ser una simple coincidencia. Bastante convincente, ¿no? Y si te dijera que estos datos en realidad reflejan un leve sesgo a favor de las mujeres (¡más o menos!), probablemente pensarías que estoy loca o que soy sexista.

Extra

Versiones anteriores de estas notas sugerían incorrectamente que Berkeley fue demandada —aparentemente eso no es cierto. Hay un buen comentario al respecto acá: https://www.refsmmat.com/posts/2016-05-08-simpsons-paradox-berkeley.html. ¡Gracias a Wilfried Van Hirtum por señalarlo!

Cuando la gente empezó a mirar los datos con más detalle (Bickel, Hammel, y O’Connell 1975), la historia resultó ser bastante diferente. En particular, cuando se analizaron los ingresos por departamento, se encontró que la mayoría de los departamentos en realidad tenían una tasa de admisión más alta para mujeres que para hombres. La siguiente tabla muestra los datos de los seis departamentos más grandes (los nombres fueron removidos por privacidad):

Departamento	Postulantes (H)	% admitidos	Postulantes (M)	% admitidas
A	825	62%	108	82%
B	560	63%	25	68%
C	325	37%	593	34%
D	417	33%	375	35%
E	191	28%	393	24%
F	272	6%	341	7%

Increíblemente, la mayoría de los departamentos admitían más mujeres (en proporción) que hombres. Sin embargo, la tasa de admisión general en toda la universidad era más baja para las mujeres. ¿Cómo puede ser? ¿Cómo pueden ser verdaderas las dos cosas al mismo tiempo?

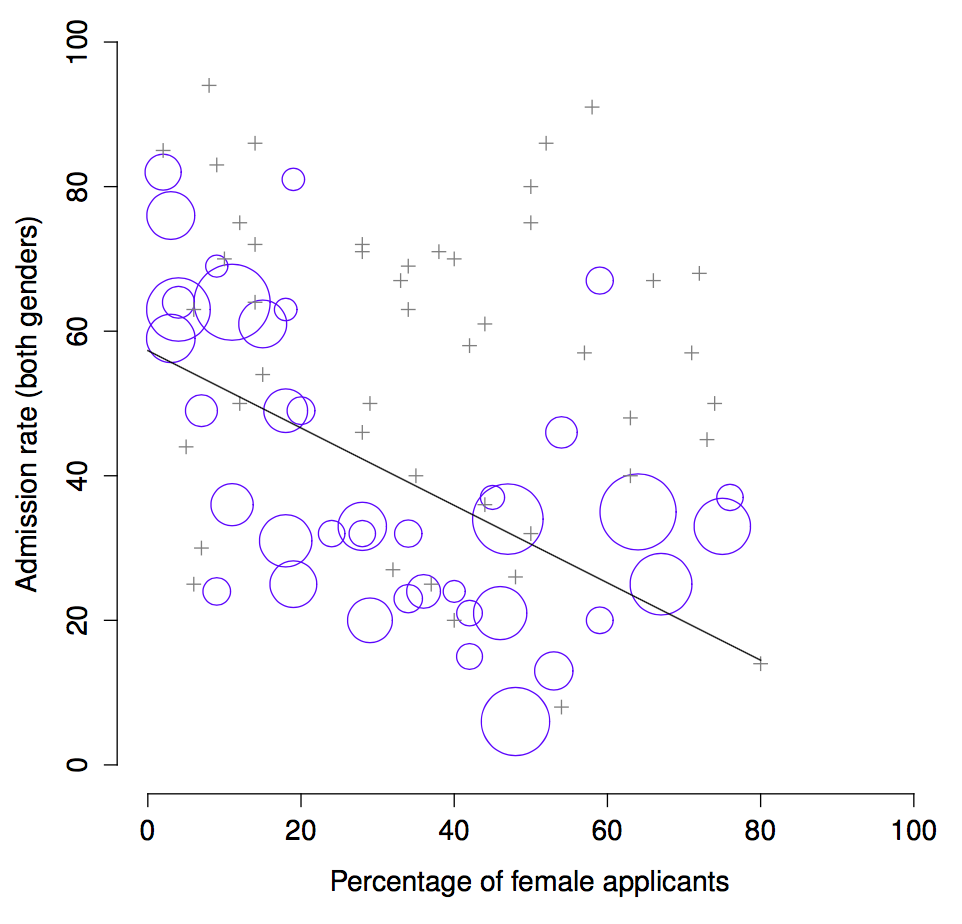
Esto es lo que pasa. Primero, notá que los departamentos no son todos iguales en cuanto a su porcentaje de admisión: algunos (como ingeniería o química) tienden a admitir a una gran parte de quienes se postulan; otros (como literatura inglesa) tienden a rechazar a la mayoría, incluso si tienen buen perfil. Así que, entre los seis departamentos de arriba, el departamento A es el más generoso, seguido por B, C, D, E y F, en ese orden. A continuación, fijate que los hombres y las mujeres tendían a postularse a departamentos diferentes. Si ordenamos los departamentos según el número total de postulaciones masculinas, obtenemos A>B>D>C>F>E (los “departamentos fáciles” están en negrita). En general, los hombres tendieron a postularse a los departamentos con tasas de admisión altas. Ahora compara esto con la distribución de las postulaciones femeninas. Clasificar los departamentos según el número total de postulaciones femeninas produce un orden bastante diferente: C>E>D>F>A>B. En otras palabras, estos datos parecen sugerir que las mujeres tendieron a postularse a departamentos “más difíciles”.

Y si miramos Figura 1.1, vemos que esta tendencia es sistemática, y bastante notable. Este fenómeno se conoce como la paradoja de Simpson. No es común, pero ocurre en la vida real, y suele sorprender muchísimo cuando uno se la encuentra por primera vez. Mucha gente incluso se niega a creer que sea real. Pero lo es. Y aunque hay muchas lecciones estadísticas sutiles escondidas acá, quiero usar este ejemplo para señalar un punto más importante: hacer investigación es difícil, y está lleno de trampas sutiles y contraintuitivas esperando a quien no esté atento. Esa es la razón #2 por la que los científiquos aman la estadística, y por la que enseñamos métodos de investigación. Porque la ciencia es difícil, y la verdad a veces está escondida en los rincones más enredados de los datos.

Figura 1.1: Datos de admisión a la universidad de Berkeley en 1973. Esta figura muestra la tasa de admisión de los 85 departamentos que recibieron al menos una postulante mujer, en función del porcentaje de postulantes que eran mujeres. El gráfico es una recreación de la Figura 1 de Bickel et al. (1975). Los círculos representan departamentos con más de 40 postulantes; el área del círculo es proporcional al número total de postulantes. Las cruces representan departamentos con menos de 40 postulantes.

Antes de dejar este tema por completo, quiero señalar algo realmente importante que muchas veces se pasa por alto en los cursos de métodos de investigación: la estadística solo resuelve parte del problema. Recordemos que todo esto empezó con la preocupación de que el proceso de admisión de Berkeley pudiera estar sesgado en contra de las mujeres. Cuando miramos los datos “agregados”, parecía que la universidad estaba discriminando. Pero cuando desagregamos y analizamos el comportamiento de los departamentos individuales, resultó que, en todo caso, había un sesgo a favor de las mujeres. El sesgo de género en las cifras totales se debía a que las mujeres tendían a postularse a los departamentos más exigentes. Desde una perspectiva legal, eso probablemente exime a la universidad. Las decisiones de admisión se toman a nivel de cada departamento (y hay buenas razones para que sea así), y a ese nivel las decisiones fueron más o menos imparciales (el leve sesgo a favor de las mujeres era pequeño y no sistemático). Como la universidad no puede decidir a qué departamento se postula cada quien, y la decisión se toma dentro del departamento, no se le puede responsabilizar por los sesgos que esas elecciones puedan producir.

Esa era la base de mis comentarios un poco superficiales más arriba, pero no es toda la historia, ¿no? Si miramos esto desde una perspectiva más sociológica o psicológica, podríamos preguntarnos por qué hay diferencias tan marcadas en las postulaciones. ¿Por qué hay más hombres postulando a ingeniería y más mujeres a literatura? ¿Y por qué los departamentos con más postulaciones femeninas tienden a tener tasas de admisión más bajas que aquellos con más postulaciones masculinas? ¿No podría eso reflejar también un sesgo de género, aunque cada departamento individual no lo tenga? Supongamos, hipotéticamente, que los hombres prefieren postularse a ciencias duras y las mujeres a humanidades. Y supongamos que las tasas bajas de admisión en humanidades se deben a que el gobierno no quiere financiarlas (por ejemplo, los cupos para doctorados suelen estar atados a proyectos con financiación estatal). ¿Eso es un sesgo de género? ¿O simplemente una visión poco iluminada sobre el valor de las humanidades? ¿Y si alguien con poder político recortó fondos para humanidades porque piensa que “son cosas de chicas, sin utilidad”? Eso ya suena claramente sesgado por género. Nada de esto lo resuelve la estadística. Pero sí importa para el proyecto de investigación. Si te interesan los efectos estructurales de sesgos de género sutiles, probablemente querrás mirar tanto los datos agregados como los desagregados. Si solo te interesa cómo se toman decisiones dentro de Berkeley, entonces solo te importan los datos desagregados.

En resumen, hay muchas preguntas fundamentales que no se responden con estadística, pero que cambian por completo cómo analizás e interpretás los datos. Y por eso deberías pensar en la estadística como una herramienta para ayudarte a entender tus datos, ni más ni menos. Es una herramienta poderosa, pero no reemplaza la reflexión cuidadosa.

1.3 Estadística en psicología

Espero que la discusión anterior haya ayudado a entender por qué la ciencia en general le da tanta importancia a la estadística. Pero seguro todavía tenés muchas preguntas sobre qué rol juega la estadística en psicología, y en especial por qué las materias de psicología tienen tantas clases dedicadas a esto. Así que acá va mi intento de responder algunas…

• ¿Por qué hay tanta estadística en psicología?

Siendo sinceros, hay varias razones, y algunas son mejores que otras. La más importante es que la psicología es una ciencia estadística. ¿Qué quiero decir con eso? Que lo que estudiamos son personas. Personas reales, complicadas, caóticas, contradictorias. La física estudia “cosas” como electrones, y aunque la física tiene sus complejidades, los electrones no tienen mente propia. No tienen opiniones, no difieren entre sí de maneras extrañas y arbitrarias, no se aburren a mitad de un experimento, y no se enojan con el experimentador para luego tratar deliberadamente de sabotear los datos (no es que yo alguna vez haya hecho eso…). A un nivel fundamental, la psicología es más difícil que la física.

Básicamente, te enseñamos estadística porque, como psicólogo, necesitás ser mejor en esto que un físico. En física a veces se dice: “si tu experimento necesita estadística, tendrías que haber hecho un mejor experimento”. Pero ellos pueden decir eso porque sus objetos de estudio son ridículamente simples comparados con el lío que enfrentamos en las ciencias sociales. No es solo psicología: casi todas las ciencias sociales dependen mucho de la estadística. No porque seamos experimentadores mediocres, sino porque elegimos problemas más difíciles. Te enseñamos estadística porque realmente la vas a necesitar.

• ¿No puede encargarse otra persona de la estadística?

Hasta cierto punto, sí, pero no completamente. No hace falta que te conviertas en un estadístico profesional para hacer psicología, pero sí necesitas alcanzar un cierto nivel de competencia estadística. Para mí, hay tres razones por las que todo investigador en psicología debería saber estadística básica:

1. La razón fundamental: la estadística está completamente ligada al diseño de investigación. Si querés diseñar buenos estudios, tenés que entender al menos lo básico.

2. En segundo lugar, si querés ser bueno en la parte psicológica de la investigación, necesitás poder entender la literatura psicológica, ¿no? Pero casi todos los artículos en esa literatura presentan resultados de análisis estadísticos. Así que, si de verdad querés entender la psicología, tenés que poder entender qué hicieron los demás con sus datos. Y eso significa saber al menos algo de estadística.

3. Ser dependiente de otros para hacer análisis estadísticos tiene un gran problema práctico: es caro. En la mayoría de los casos no vas a tener presupuesto para contratar un estadístico. Así que, por economía, tenés que poder arreglártelas por tu cuenta.

Y ojo, esto no aplica solo a investigadores. Si querés ejercer como psicólogo y mantenerte al día, te conviene poder leer la literatura científica, que está llena de estadística.

• No me interesan ni los trabajos, ni la investigación, ni lo clínico. ¿Igual necesito estadística?

Ahora ya me estás tomando el pelo. Pero igual te debería importar. La estadística te debería importar como le debería importar a todo el mundo: vivimos en el siglo XXI, y los datos están por todos lados. Honestamente, con el mundo como está hoy, saber un poco de estadística es casi una herramienta de supervivencia.

Y eso nos lleva al próximo tema…

1.4 Estadística en la vida cotidiana

“Nos estamos ahogando en información,
pero nos morimos de hambre por conocimiento”

– Varios autores, original probablemente de John Naisbitt

Cuando empecé a escribir estas notas, tomé los 20 artículos más recientes del sitio de noticias de ABC. De esos 20, resultó que 8 trataban sobre algo que yo consideraría un tema estadístico; 6 de esos 8 tenían algún error. El error más común, por si te da curiosidad, era no reportar datos de línea de base (por ejemplo, el artículo dice que el 5% de las personas en la situación X tienen cierta característica Y, pero no dice cuán común es esa característica en la población general). El punto no es que los periodistas sean malísimos en estadística (aunque casi siempre lo son), sino que tener un conocimiento básico de estadística te ayuda mucho para darte cuenta cuando alguien se equivoca —o directamente te está mintiendo. Quizás, una de las mayores consecuencias de aprender estadística es que te vas a enojar con el diario o con internet mucho más seguido :).

1.5 Hay más en los métodos de investigación que solo la estadística

Hasta ahora, la mayoría de lo que dije fue sobre estadística, así que no te culpo si pensás que es lo único que me importa en la vida. Para ser justos, no estarías tan equivocado, pero la metodología de investigación es un concepto más amplio. Por eso, los cursos de métodos suelen cubrir un montón de temas más ligados a los aspectos prácticos del diseño de investigaciones, especialmente cuando trabajás con personas. Sin embargo, el 99% de los miedos estudiantiles tienen que ver con la parte estadística del curso, así que me enfoqué en eso, y espero haberte convencido de que la estadística importa, y más importante aún, que no hay que tenerle miedo. Dicho eso, es bastante típico que los cursos introductorios de métodos estén muy cargados de estadística. Y no es (generalmente) porque los docentes sean gente malvada. Al contrario. Los cursos introductorios se enfocan tanto en estadística porque la vas a necesitar antes que el resto del entrenamiento metodológico. ¿Por qué? Porque en casi todas tus otras materias, los trabajos prácticos van a requerir análisis estadístico, mucho más que cualquier otra herramienta de metodología. No es común que te pidan diseñar un estudio desde cero (en cuyo caso sí necesitarías saber mucho sobre diseño de investigación), pero sí es común que te pidan analizar e interpretar datos recolectados por otra persona (en cuyo caso necesitás estadística). En ese sentido, si pensás en lo que más te va a servir para rendir bien en tus materias, la estadística es lo más urgente.

Pero tené en cuenta que “urgente” es diferente de “importante”; ambos son relevantes. De verdad quiero insistir en que el diseño de investigación es tan importante como el análisis de datos, y este libro le dedica bastante espacio. Aun así, mientras que la estadística tiene un carácter más universal y te da un conjunto de herramientas útiles para casi cualquier investigación en psicología, el diseño de investigación no es tan generalizable. Hay principios básicos que todos deberían tener en cuenta, pero muchos aspectos del diseño son muy específicos del área en la que trabajás. Y como lo que más importa está en los detalles, esos detalles casi nunca aparecen en un curso introductorio de estadística y métodos.

1.6 Una breve introducción al diseño de investigación

En este capítulo vamos a empezar a pensar en las ideas básicas que intervienen al diseñar un estudio, recolectar datos, verificar si la recolección funciona, etc. No te va a dar suficiente info como para que puedas diseñar tus propios estudios, pero sí te va a dar herramientas básicas para evaluar los estudios de otros. Sin embargo, como este libro está más enfocado en el análisis de datos que en la recolección, solo voy a dar un panorama general.

Este capítulo es “especial” por dos razones. Primero, es mucho más específico de la psicología que los capítulos que vienen después. Segundo, se enfoca mucho más en el problema científico del diseño metodológico, y mucho menos en el problema estadístico del análisis de datos. De todos modos, los dos problemas están relacionados entre sí, así que es común que los libros de estadística los traten con cierto detalle.

Este capítulo se basa bastante en Campbell y Stanley (1963) para el diseño de estudios, y en Stevens (1946) para la discusión sobre escalas de medición.

1.7 Introducción a la medición psicológica

Lo primero que hay que entender es que la recolección de datos puede pensarse como una forma de medición. Es decir, lo que estamos tratando de hacer acá es medir algo sobre el comportamiento o la mente humana. ¿Qué quiero decir con “medición”?

1.7.1 Algunas ideas sobre la medición psicológica

La medición es un concepto sutil, pero básicamente se trata de encontrar una forma de asignar números, etiquetas u otras descripciones bien definidas a “cosas”. Así que, cualquiera de los siguientes ejemplos cuenta como una medición psicológica:

• Mi edad es 33 años.

• No me gustan las anchoas.

• Mi sexo cromosómico es masculino.

• Mi género autoidentificado es masculino.

En esta lista, lo que está en negrita es “lo que se quiere medir”, y lo que está en cursiva es “la medida en sí”. Podemos ir un poco más allá y pensar en el conjunto de posibles mediciones que podrían haber surgido en cada caso:

• Mi edad (en años) podría haber sido 0, 1, 2, 3… etc. El límite superior de lo que podría ser mi edad es un poco impreciso, pero en la práctica podrías decir tranquilamente que la edad máxima posible es 150, ya que ningún ser humano ha vivido tanto.

• Al preguntarme si me gustan las anchoas, podría haber respondido sí, no, no tengo opinión, o a veces.

• Mi sexo cromosómico casi seguro será masculino (XY) o femenino (XX), pero hay otras posibilidades, como el síndrome de Klinefelter (XXY), que es más similar al masculino. Y seguro hay más posibilidades.

• Mi género autoidentificado también podría ser masculino o femenino, pero no tiene por qué coincidir con el sexo cromosómico. También podría identificarme con ninguno, o declararme explícitamente transgénero.

Como ves, para algunas cosas (como la edad) es bastante claro cuál es el conjunto de valores posibles, pero para otras se vuelve más complicado. Incluso con la edad, hay sutilezas. En el ejemplo anterior asumí que medir en años estaba bien. Pero si sos psicólogo del desarrollo, eso es muy burdo: se suele usar años y meses (por ejemplo, “2;11” para 2 años y 11 meses). Si trabajás con recién nacidos, tal vez necesites medir días desde el nacimiento, o incluso horas.

Y si lo pensás más, te das cuenta de que el concepto de “edad” no es tan preciso. En general, cuando decimos “edad” nos referimos al tiempo desde el nacimiento. Pero eso no siempre es lo ideal. Supongamos que te interesa estudiar el control ocular en recién nacidos. En ese caso, podrías cuestionarte si “nacimiento” es el punto de referencia adecuado. Si María nace 3 semanas antes de término y Juana una semana después, ¿tienen la “misma edad” si las observamos a las 2 horas de nacidas? Socialmente, sí. Pero desde una perspectiva biológica, no. Tal vez convenga definir dos conceptos distintos: tiempo desde la concepción, y tiempo desde el nacimiento. Para adultos no hace diferencia, pero para recién nacidos sí.

Más allá de eso, está la cuestión metodológica: ¿qué “método de medición” vas a usar para averiguar la edad? Como antes, hay muchas posibilidades.

• Podés simplemente preguntar: “¿cuántos años tenés?” El autorreporte es rápido, barato y sencillo, pero solo sirve con personas lo suficientemente grandes como para entender la pregunta, y alguna gente miente sobre su edad.

• Podrías preguntarle a una persona referente (por ejemplo, a la madre o al padre): “¿Qué edad tiene tu hijo?” Este método es rápido, y cuando se trata de niños no suele ser complicado, ya que casi siempre hay algún adulto presente. No funciona tan bien si querés saber la “edad desde la concepción”, porque muchas veces los padres no saben con certeza cuándo ocurrió. Para eso, quizás necesites otra autoridad (por ejemplo, un obstetra).

• Podés consultar registros oficiales, como partidas de nacimiento. Es un proceso tedioso y lleva tiempo, pero puede ser útil (por ejemplo, si la persona ya falleció).

1.7.2 Operacionalización: definir tu medición

Todas las ideas discutidas en la sección anterior se relacionan con el concepto de operacionalización. Para ser un poco más precisos, es el proceso de tomar un concepto significativo pero vago, y convertirlo en una medición precisa. La operacionalización puede incluir varias cosas diferentes:

• Ser preciso sobre qué intentás medir. Por ejemplo, ¿“edad” significa tiempo desde el nacimiento o desde la concepción en el contexto de tu investigación?

• Definir el método que vas a usar. ¿Vas a usar autorreporte, le vas a preguntar a alguien más, o vas a consultar registros? Y si usás autorreporte, ¿cómo vas a formular la pregunta?

• Definir el conjunto de valores permitidos: Tené en cuenta que estos valores no siempre tienen que ser numéricos, aunque muchas veces lo son. Al medir la edad, los valores son numéricos, pero aún así necesitamos pensar bien qué números vamos a permitir. ¿Queremos la edad en años, en años y meses, en días, en horas? Y así. Para otros tipos de mediciones (por ejemplo, el género), los valores no son numéricos. Pero, como antes, tenemos que pensar qué valores vamos a permitir. Si les pedimos a las personas que autoinformen su género, ¿qué opciones les vamos a ofrecer? ¿Alcanza con permitir solo “masculino” o “femenino”? ¿Necesitamos una opción de “otro”? ¿O sería mejor no dar opciones cerradas y dejar que respondan con sus propias palabras? Y si abrimos el conjunto de valores posibles para incluir todas las respuestas verbales, ¿cómo vamos a interpretar sus respuestas?

La operacionalización no es una tarea sencilla, y no existe una única manera “correcta” de llevarla a cabo. La forma en que elijas operacionalizar un concepto informal como “edad” o “género” en una medición formal depende del uso que vayas a darle a esa medición. A menudo, vas a encontrar que la comunidad científica que trabaja en tu área ya tiene ideas bastante consolidadas sobre cómo hacerlo. En otras palabras, la operacionalización debe pensarse caso por caso. Dicho esto, aunque hay muchos aspectos que dependen del proyecto de investigación particular, también hay elementos que son bastante generales.

Antes de continuar, quiero detenerme un momento para aclarar algunos términos y, de paso, introducir uno más. A continuación, presento cuatro conceptos estrechamente relacionados entre sí:

• Un constructo teórico: es lo que querés medir, como “edad”, “género” u “opinión”. No se puede observar directamente, y suele ser algo vago.

• Una medida: es el método o herramienta que usás para hacer tus observaciones. Puede ser una pregunta en una encuesta, una observación conductual o una resonancia.

• Una operacionalización: es la conexión lógica entre el constructo y la medida, o el proceso por el cual derivás una medida a partir del constructo teórico.

• Una variable: Finalmente, un término nuevo: una variable es lo que obtenemos cuando aplicamos una medida a algo del mundo real. Es decir, las variables son los datos concretos que terminamos registrando en nuestros conjuntos de datos.

En la práctica, incluso los científicos tienden a mezclar estos términos, pero es muy útil tratar de comprender en qué se distinguen.

1.7.3 Escalas de medición

Como vimos en la sección anterior, el resultado de una medición psicológica se llama variable. Pero no todas las variables son del mismo tipo cualitativo, y es muy útil entender qué tipos existen. Un concepto muy útil para distinguir entre tipos de variables es el de escalas de medición.

1.7.4 Escala nominal

Una variable de escala nominal (también llamada categórica) es aquella en la que no hay una relación particular entre las distintas opciones: para este tipo de variables no tiene sentido decir que una es “mayor” o “mejor” que otra, y mucho menos calcular un promedio. El ejemplo clásico es el “color de ojos”. Pueden ser azules, verdes o marrones, entre otras opciones, pero ninguna es mejor que otra. Por eso sería raro hablar de un “color de ojos promedio”. Lo mismo pasa con el género: ser hombre no es mejor ni peor que ser mujer, y no tiene sentido hablar de un “género promedio”. En resumen, las variables nominales son aquellas en las que lo único que podés decir es que las categorías son diferentes. Y nada más.

Veamos esto más de cerca. Supongamos que estoy investigando cómo viaja la gente al trabajo. Una variable que tendría que medir es el medio de transporte. Esta variable “medio de transporte” podría incluir varios valores, incluyendo: “tren”, “ómnibus”, “auto”, “bicicleta”, etc. Supongamos por ahora que esas cuatro son las únicas opciones, y que al preguntar a 100 personas cómo llegaron hoy al trabajo, obtengo esto:

Medio de transporte	Cantidad de personas
(1) Tren	12
(2) Ómnibus	30
(3) Auto	48
(4) Bicicleta	10

Entonces, ¿cuál es el medio de transporte promedio? Obviamente, no lo hay. Es una pregunta sin sentido. Podés decir que el auto es el medio más popular y que el tren es el menos popular, pero nada más. Fijate además que el orden en que puse las opciones no importa mucho. Podría haber presentado los datos así, y nada cambia realmente:

Medio de transporte	Cantidad de personas
(3) Auto	48
(1) Tren	12
(4) Bicicleta	10
(2) Ómnibus	30

1.7.5 Escala ordinal

Las variables de escala ordinal tienen un poco más de estructura que las variables de escala nominal, pero no mucho más. Una variable ordinal es aquella en la que hay una forma natural y significativa de ordenar las distintas opciones, pero no se puede hacer mucho más. El ejemplo habitual es la “posición de llegada en una carrera”. Podés decir que la persona que llegó primera fue más rápida que la que llegó segunda, pero no sabés cuánto más rápida. Como consecuencia, sabemos que 1.º \(>\) 2.º y que 2.º \(>\) 3.º, pero la diferencia entre 1.º y 2.º podría ser mucho mayor que la diferencia entre 2.º y 3.º.

Acá hay un ejemplo más interesante desde el punto de vista psicológico. Supongamos que me interesa conocer las actitudes de las personas frente al cambio climático, y les pido que elijan una de estas cuatro afirmaciones, la que más se acerque a sus creencias:

1. Las temperaturas están subiendo debido a la actividad humana
2. Las temperaturas están subiendo, pero no sabemos por qué
3. Las temperaturas están subiendo, pero no por causa humana
4. Las temperaturas no están subiendo

Fijate que estas cuatro afirmaciones tienen un orden natural, en cuanto al “grado en que coinciden con el consenso científico actual”. La afirmación 1 coincide completamente, la 2 coincide de forma razonable, la 3 no coincide mucho, y la 4 está en fuerte desacuerdo con la ciencia. Así que, en relación con lo que me interesa (el grado en que la gente avala la ciencia), puedo ordenarlas como 1 \(>\) 2 \(>\) 3 $>$4. Por eso, sería muy raro listar las opciones así…

3. Las temperaturas están subiendo, pero no por causa humana
4. Las temperaturas están subiendo debido a la actividad humana
5. Las temperaturas no están subiendo
6. Las temperaturas están subiendo, pero no sabemos por qué

…porque parece violar la “estructura” natural de la pregunta.

Ahora supongamos que les hago esta pregunta a 100 personas y obtengo las siguientes respuestas:

	Personas
(1) Las temperaturas están subiendo debido a la actividad humana	51
(2) Las temperaturas están subiendo, pero no sabemos por qué	20
(3) Las temperaturas están subiendo, pero no por causa humana	10
(4) Las temperaturas no están subiendo	19

Al analizar estos datos, parece bastante razonable agrupar las respuestas (1), (2) y (3), y decir que 81 de 100 personas están dispuestas a al menos en parte avalar la ciencia. Y también es razonable agrupar (2), (3) y (4), y decir que 49 de 100 expresan al menos cierto desacuerdo con el consenso científico. Pero sería completamente extraño agrupar (1), (2) y (4) y decir que 90 de 100 personas dijeron… ¿qué? No hay nada sensato que permita agrupar esas respuestas.

Dicho eso, aunque sí podemos usar el orden natural de estas opciones para construir agrupamientos sensatos, lo que no podemos hacer es promediarlas. Por ejemplo, en este caso, la respuesta “promedio” sería 1.97. Si podés explicarme qué significa eso, me encantaría saberlo. ¡Porque a mí me suena a puro disparate!

1.7.6 Escala de intervalo

A diferencia de las variables de escala nominal y ordinal, las variables de escala de intervalo y de razón son aquellas en las que el valor numérico tiene un significado genuino. En el caso de las variables de escala de intervalo, las diferencias entre los números son interpretables, pero la variable no tiene un valor cero “natural”. Un buen ejemplo de una variable de escala de intervalo es la temperatura medida en grados Celsius. Por ejemplo, si ayer hizo 15 °C y hoy hace 18 °C, la diferencia de 3 °C entre ambos días tiene un significado real. Además, esa diferencia de 3 °C es exactamente la misma que la diferencia entre 7 °C y 10 °C. En resumen, la suma y la resta tienen sentido para variables de escala de intervalo.

Sin embargo, notá que 0 °C no significa “ausencia total de temperatura”: en realidad significa “la temperatura a la que se congela el agua”, lo cual es bastante arbitrario. Como consecuencia, resulta inútil intentar multiplicar o dividir temperaturas. Está mal decir que 20 °C es el doble de caliente que 10 °C, así como también es raro y carece de sentido decir que 20 °C es “menos dos veces más caliente” que –10 °C.

Veamos otro ejemplo más relacionado con la psicología. Supongamos que me interesa estudiar cómo han cambiado las actitudes de los estudiantes de primer año de universidad a lo largo del tiempo. Obviamente, voy a querer registrar el año en que cada estudiante ingresó. Ese año es una variable de escala de intervalo. Un estudiante que ingresó en 2003 lo hizo cinco años antes que uno que ingresó en 2008. Sin embargo, sería completamente absurdo dividir 2008 entre 2003 y decir que la segunda persona ingresó “1,0024 veces más tarde” que la primera. Eso no tiene ningún sentido.

---

1.7.7 Escala de razón

El cuarto y último tipo de variable que vamos a considerar es la variable de escala de razón, en la cual el cero realmente significa cero, y está bien multiplicar y dividir. Un buen ejemplo psicológico de una variable de escala de razón es el tiempo de respuesta. En muchas tareas es común registrar cuánto tiempo le lleva a alguien resolver un problema o responder una pregunta, ya que eso puede ser un indicador de cuán difícil es la tarea. Supongamos que Alan tarda 2,3 segundos en responder una pregunta, mientras que Ben tarda 3,1 segundos. Al igual que con una variable de escala de intervalo, la suma y la resta tienen sentido: Ben realmente tardó (3{,}1 - 2{,}3 = 0{,}8) segundos más que Alan. Sin embargo, también tiene sentido multiplicar y dividir: Ben tardó (3{,}1 / 2{,}3 = 1{,}35) veces más que Alan en responder. Y esto tiene sentido porque, para una variable de escala de razón como el tiempo de respuesta, “cero segundos” realmente significa “ningún tiempo en absoluto”.

---

1.7.8 Variables continuas versus discretas

Hay otro tipo de distinción que tenés que tener en cuenta respecto a los tipos de variables con los que podés encontrarte. Es la distinción entre variables continuas y variables discretas. La diferencia es la siguiente:

• Una variable continua es aquella en la que, entre cualquier par de valores que se te ocurra, siempre es lógicamente posible que exista otro valor intermedio.

• Una variable discreta es, en efecto, una variable que no es continua. En una variable discreta, a veces no hay nada en el medio.

Estas definiciones pueden parecer un poco abstractas, pero son bastante simples una vez que ves algunos ejemplos. Por ejemplo, el tiempo de respuesta es una variable continua. Si Alan tarda 3,1 segundos y Ben tarda 2,3 segundos en responder una pregunta, entonces es posible que Cameron haya tardado 3,0 segundos, es decir, un valor intermedio. Y claro, también sería posible que David tardara 3,031 segundos, lo que lo pondría entre Cameron y Alan. Aunque en la práctica tal vez no podamos medir el tiempo de respuesta con tanta precisión, en principio sí se puede. Como siempre es posible encontrar un nuevo valor entre cualquier par de valores, decimos que el tiempo de respuesta es una variable continua.

Las variables discretas aparecen cuando esta regla se rompe. Por ejemplo, las variables de escala nominal son siempre discretas: no hay un medio de transporte que esté “entre” el tren y la bicicleta, al menos no de la manera estrictamente matemática en la que 2,3 está entre 2 y 3. Así que el tipo de transporte es una variable discreta. Del mismo modo, las variables ordinales también son siempre discretas: aunque el “2.º lugar” esté entre el “1.º” y el “3.º”, no hay nada que pueda caer entre el 1.º y el 2.º lugar. Las variables de escala de intervalo y de razón pueden ser continuas o discretas. Como vimos antes, el tiempo de respuesta (una variable de razón) es continua. La temperatura en grados Celsius (una variable de intervalo) también es continua. Pero el año en que alguien ingresó a la universidad (una variable de intervalo) es discreta: no hay ningún año entre 2002 y 2003. El número de respuestas correctas en un test de verdadero/falso (una variable de razón) también es discreto: como una pregunta de verdadero/falso no permite estar “parcialmente correcto”, no hay nada entre 5/10 y 6/10.

La siguiente tabla resume la relación entre las escalas de medición y la distinción continuo/discreto. Las celdas con una “x” marcan combinaciones posibles. Estoy tratando de dejar bien en claro este punto porque: (a) algunos manuales no lo explican bien, y (b) muy seguido la gente dice cosas como “variable discreta” cuando en realidad quiere decir “variable de escala nominal”. Es una confusión bastante desafortunada.

	continua	discreta
nominal		x
ordinal		x
intervalo	x	x
razón	x	x

Relación entre las escalas de medición y la distinción continuo/discreto. Las celdas con “x” marcan combinaciones posibles.

1.7.9 Algunas complejidades

Bueno, sé que esto te va a sorprender, pero… el mundo real es mucho más desordenado de lo que sugiere esta pequeña clasificación. Muy pocas variables en la vida real encajan perfectamente en estas categorías ordenadas, así que hay que tener cuidado de no tratar las escalas de medición como si fueran reglas rígidas. No funcionan así: son guías pensadas para ayudarte a reflexionar sobre en qué situaciones conviene tratar a las variables de manera diferente. Nada más.

Así que tomemos un ejemplo clásico, quizás el ejemplo clásico, de una herramienta de medición psicológica: la escala de Likert. La humilde escala de Likert es el pan de cada día en el diseño de encuestas. Vos mismo habrás completado cientos, tal vez miles, y probablemente ya usaste una. Supongamos que tenés una pregunta en una encuesta que se ve así:

¿Cuál de las siguientes opciones describe mejor tu opinión sobre la afirmación: “todos los piratas son increíblemente geniales”?

Y luego se le presentan al participante las siguientes opciones:

1. Totalmente en desacuerdo
   
2. En desacuerdo
   
3. Ni de acuerdo ni en desacuerdo
   
4. De acuerdo
   
5. Totalmente de acuerdo

Este conjunto de ítems es un ejemplo de una escala de Likert de 5 puntos: se le pide a la gente que elija entre una de varias (en este caso 5) posibilidades claramente ordenadas, generalmente con una descripción verbal en cada caso. Sin embargo, no es necesario que todos los ítems estén explícitamente etiquetados. Este también es un ejemplo perfectamente válido de una escala de Likert de 5 puntos:

1. Totalmente en desacuerdo
   
5. Totalmente de acuerdo

Las escalas de Likert son herramientas muy útiles, aunque algo limitadas. La pregunta es: ¿qué tipo de variable son? Obviamente son discretas, ya que no se puede responder “2,5”. Claramente no son de escala nominal, porque los ítems están ordenados; y tampoco son de escala de razón, porque no hay un cero natural.

Pero entonces, ¿son de escala ordinal o de intervalo? Un argumento sostiene que no podemos realmente demostrar que la diferencia entre “totalmente de acuerdo” y “de acuerdo” sea del mismo tamaño que la diferencia entre “de acuerdo” y “ni de acuerdo ni en desacuerdo”. De hecho, en la vida cotidiana es bastante obvio que no son iguales. Esto sugiere que deberíamos tratar las escalas de Likert como variables ordinales. Por otro lado, en la práctica, la mayoría de los participantes parece tomarse bastante en serio eso de “en una escala del 1 al 5”, y tienden a comportarse como si las diferencias entre las cinco opciones de respuesta fueran más o menos similares entre sí. Como consecuencia, muchos investigadores tratan los datos de escalas de Likert como si fueran de escala de intervalo. No lo son realmente, pero en la práctica se parecen lo suficiente como para que usualmente pensemos en ellas como de cuasi-escala de intervalo.

1.8 Evaluación de la confiabilidad de una medición

A esta altura ya reflexionamos un poco sobre cómo operacionalizar un constructo teórico y, a partir de eso, construir una medida psicológica; y vimos que, al aplicar esas medidas, terminamos con variables, que pueden ser de muchos tipos distintos. En este punto, deberíamos empezar a discutir la pregunta obvia: ¿la medición es buena? Vamos a abordarlo en términos de dos ideas relacionadas: confiabilidad y validez. En términos simples, la confiabilidad de una medida te dice cuán precisamente estás midiendo algo, mientras que la validez te dice cuán exacta es esa medida.

La confiabilidad es en realidad un concepto muy simple: se refiere a la repetibilidad o consistencia de tu medición. Medir mi peso con una balanza de baño es muy confiable: si me subo y bajo varias veces, va a seguir marcando lo mismo. Medir mi inteligencia preguntándole a mi mamá no es nada confiable: algunos días me dice que soy medio lenta, y otros días que soy una completa idiota. Fijate que este concepto de confiabilidad es distinto de la cuestión de si la medición es correcta (la exactitud de una medición tiene que ver con su validez, no con su confiabilidad). Si estoy sosteniendo una bolsa de papas al subirme y bajarme de la balanza del baño, la medición seguirá siendo confiable: siempre me va a dar el mismo número. Sin embargo, esta respuesta altamente confiable no se corresponde en absoluto con mi peso real, por lo tanto está equivocada. En términos técnicos, esta es una medición confiable pero inválida. De forma similar, aunque la estimación que hace mi mamá de mi inteligencia sea poco confiable, podría tener razón. Tal vez simplemente no soy muy brillante, y aunque su estimación fluctúe bastante de un día a otro, en esencia sea correcta. Eso sería una medida inválida pero confiable. Claro que, hasta cierto punto, si las estimaciones de mi mamá son demasiado inconsistentes, va a ser muy difícil saber cuál de todas sus opiniones sobre mi inteligencia es la verdadera. En ese sentido, una medición muy poco confiable tiende a terminar siendo inválida en la práctica; tanto así que muchos dirían que la confiabilidad es necesaria (aunque no suficiente) para garantizar la validez.

Bien, ahora que tenemos clara la distinción entre confiabilidad y validez, pensemos en las distintas maneras en que podemos medir la confiabilidad:

• Confiabilidad test-retest. Se refiere a la consistencia en el tiempo: si repetimos la medición más adelante, ¿obtenemos la misma respuesta?
• Confiabilidad entre evaluadores (inter-rater reliability). Se refiere a la consistencia entre personas: si otra persona repite la medición (por ejemplo, si otra persona evalúa mi inteligencia), ¿obtiene la misma respuesta?
• Confiabilidad de formas paralelas. Se refiere a la consistencia entre mediciones teóricamente equivalentes: si uso otra balanza para pesarme, ¿marca lo mismo?
• Confiabilidad de consistencia interna. Si una medición está compuesta por muchas partes que cumplen funciones similares (por ejemplo, una escala de personalidad que suma varias preguntas), ¿tienden esas partes a dar resultados similares?

No todas las mediciones necesitan cumplir todas las formas de confiabilidad. Por ejemplo, la evaluación educativa puede pensarse como una forma de medición. En una de las materias que enseño, Ciencia Cognitiva Computacional, la estructura de evaluación incluye un componente de investigación y un examen (entre otras cosas). El examen está diseñado para medir algo diferente al componente de investigación, así que la evaluación total tiene una baja consistencia interna. Sin embargo, dentro del examen hay varias preguntas que están pensadas para medir más o menos lo mismo, y esas tienden a producir resultados similares; por lo tanto, el examen por sí solo tiene una consistencia interna bastante alta. Que es como debería ser. Solo deberías exigir confiabilidad cuando realmente querés medir la misma cosa.

1.9 El rol de las variables: predictoras y dependientes

Bien, me queda una última pieza de terminología que necesito explicarte antes de dejar atrás el tema de las variables. Normalmente, cuando hacemos una investigación terminamos con muchas variables distintas. Luego, cuando analizamos nuestros datos, usualmente tratamos de explicar algunas de esas variables en función de otras. Es importante mantener bien separadas las dos funciones: la “que explica” y la “que es explicada”. Así que dejemos esto claro desde ahora.

Primero, conviene ir acostumbrándonos a la idea de usar símbolos matemáticos para describir variables, porque lo vamos a hacer muchas veces. Vamos a denotar la variable “que queremos explicar” como \(Y\), y las variables “que la explican” como \(X_1\), \(X_2\), etc.

Ahora bien, cuando hacemos un análisis, usamos nombres diferentes para \(X\) e \(Y\), ya que cumplen distintos roles. Los nombres clásicos para estos roles son variable independiente (VI) y variable dependiente (VD). La VI es la que usamos para explicar (es decir, \(X\)), y la VD es la que queremos explicar (es decir, \(Y\)). La lógica detrás de estos nombres es algo así: si hay una relación entre \(X\) e \(Y\), entonces podemos decir que \(Y\) depende de \(X\), y si el estudio está bien diseñado, entonces \(X\) no depende de nada más. Sin embargo, personalmente encuentro estos nombres horribles: son difíciles de recordar y muy engañosos, porque (a) la VI nunca es realmente “independiente de todo lo demás”, y (b) si no hay relación, entonces la VD no depende de la VI. Y de hecho, como no soy la única que piensa que “VI” y “VD” son nombres espantosos, hay varias alternativas que me parecen más acertadas.

Por ejemplo, en un experimento, la VI se refiere a la manipulación, y la VD a la medición. Así que podríamos usar variable manipulada (para la independiente) y variable medida (para la dependiente).

Terminología utilizada para distinguir los distintos roles que puede cumplir una variable en el análisis de datos.

Rol de la variable	Nombre clásico	Nombre moderno
“la que se explica”	variable dependiente (VD)	Medición
“la que explica”	variable independiente (VI)	Manipulación

También podríamos usar predictoras y resultados. La idea es que tratamos de usar \(X\) (las predictoras) para hacer conjeturas sobre \(Y\) (los resultados). Esto se resume en la siguiente tabla:

Terminología utilizada para distinguir los distintos roles que puede cumplir una variable en el análisis de datos.

Rol de la variable	Nombre clásico	Nombre moderno
“la que se explica”	variable dependiente (VD)	resultado
“la que explica”	variable independiente (VI)	predictora

1.10 Investigación experimental y no experimental

Una de las grandes distinciones que conviene tener presente es la diferencia entre “investigación experimental” e “investigación no experimental”. Cuando hacemos esta distinción, en realidad estamos hablando del grado de control que tiene la persona investigadora sobre los participantes y los eventos del estudio.

1.10.1 Investigación experimental

La característica clave de la investigación experimental es que la persona investigadora controla todos los aspectos del estudio, especialmente lo que los participantes experimentan durante el mismo. En particular, manipula o varía algo (las variables independientes), y luego deja que la variable dependiente varíe de forma natural. La idea es variar deliberadamente algo en el mundo (la VI) para ver si eso tiene algún efecto causal sobre los resultados. Además, para asegurarse de que no haya otra cosa, aparte de la variable manipulada, causando los resultados, todo lo demás se mantiene constante o se “balancea” de alguna manera para que no afecte el experimento. En la práctica, es casi imposible pensar en todas las demás cosas que podrían influir en los resultados de un experimento, y mucho menos mantenerlas constantes. La solución estándar para esto es la aleatorización: es decir, asignar al azar a las personas a distintos grupos, y luego darle a cada grupo un tratamiento distinto (es decir, asignarles distintos valores de las variables predictoras). Hablaremos más de la aleatorización más adelante en el curso, pero por ahora alcanza con decir que lo que hace la aleatorización es minimizar (aunque no eliminar) las probabilidades de que haya diferencias sistemáticas entre los grupos.

Veamos un ejemplo muy simple, completamente irreal y groseramente antiético. Supongamos que querés averiguar si fumar causa cáncer de pulmón. Una forma de hacerlo sería encontrar personas que fuman y personas que no fuman, y ver si les fumadores tienen una tasa más alta de cáncer de pulmón. Esto no es un experimento propiamente dicho, porque la persona investigadora no tiene mucho control sobre quién fuma y quién no. Y eso importa: por ejemplo, podría ser que quienes eligen fumar también tiendan a tener dietas poco saludables, o que trabajen en minas de asbesto, o lo que sea. El punto es que los grupos (fumadores y no fumadores) difieren en muchas cosas, no solo en fumar. Así que podría ser que la mayor incidencia de cáncer de pulmón entre fumadores se deba a otra cosa, y no al tabaquismo en sí. En términos técnicos, esas otras cosas (como la dieta) se llaman “confusores” (o confounds, en inglés), y hablaremos de eso en un momento.

Mientras tanto, veamos cómo sería un experimento propiamente dicho. Recordá que nuestra preocupación era que fumadores y no fumadores podrían diferir en muchas cosas. La solución —siempre y cuando no tengas ética— es controlar quién fuma y quién no. Específicamente, si dividimos aleatoriamente a los participantes en dos grupos, y forzamos a la mitad a convertirse en fumadores, entonces es muy poco probable que los grupos difieran en otra cosa aparte del hecho de que la mitad fuma. De ese modo, si el grupo que fuma desarrolla cáncer a una tasa más alta que el grupo que no fuma, entonces podemos tener bastante confianza en que (a) fumar sí causa cáncer y (b) somos asesinos.

1.10.2 Investigación no experimental

La investigación no experimental es un término amplio que abarca “cualquier estudio en el que la persona investigadora no tiene tanto control como en un experimento”. Obviamente, tener control es algo que los científicos suelen querer, pero como ilustra el ejemplo anterior, hay muchas situaciones en las que no podés (o no deberías) intentar ejercer ese control. Ya que es profundamente antiético (y casi con certeza ilegal) forzar a alguien a fumar para ver si desarrolla cáncer, este es un buen ejemplo de una situación en la que definitivamente no deberías tratar de controlar experimentalmente. Pero también hay otras razones. Incluso dejando de lado las cuestiones éticas, nuestro “experimento del tabaco” tiene algunos problemas más. Por ejemplo, cuando sugerí que forzáramos a la mitad de los participantes a fumar, estaba hablando de empezar con una muestra de personas no fumadoras, y luego forzarlas a convertirse en fumadoras. Si bien esto suena como el sólido y perverso diseño experimental que disfrutaría un científico loco, tal vez no sea una manera muy válida de investigar el efecto en el mundo real. Supongamos, por ejemplo, que fumar solo causa cáncer de pulmón cuando las personas tienen dietas poco saludables, y que además quienes normalmente fuman tienden a tener dietas poco saludables. Sin embargo, como en nuestro experimento los “fumadores” no son fumadores “naturales” (es decir, forzamos a personas no fumadoras a empezar a fumar, sin que adoptaran todas las demás características típicas de los fumadores en la vida real), es probable que tengan mejores dietas. Como resultado, en este ejemplo tonto, puede que no desarrollen cáncer de pulmón, y entonces nuestro experimento fallaría, porque viola la estructura del mundo “natural” (el nombre técnico de esto es un resultado “artefactual”; ya hablaremos de eso más adelante).

Una distinción útil entre dos tipos de investigación no experimental es la diferencia entre la investigación cuasi-experimental y los estudios de caso. El ejemplo que discutimos antes —en el que queremos examinar la incidencia de cáncer de pulmón entre fumadores y no fumadores, sin controlar quién fuma y quién no— es un diseño cuasi-experimental. Es decir, se parece a un experimento, pero no controlamos las variables predictoras (VIs). Igual podemos usar estadísticas para analizar los resultados, solo que tenemos que ser mucho más cuidadosos.

La alternativa, los estudios de caso, apuntan a brindar una descripción muy detallada de uno o unos pocos casos. En general, no se pueden usar estadísticas para analizar los resultados de estudios de caso, y usualmente es muy difícil sacar conclusiones generales sobre “la gente en general” a partir de unos pocos ejemplos aislados. Sin embargo, los estudios de caso son muy útiles en algunas situaciones. Primero, hay ocasiones en las que no tenés otra alternativa: la neuropsicología se encuentra con esto todo el tiempo. A veces no se puede encontrar muchas personas con daño cerebral en una zona específica, así que lo único que podés hacer es describir con el mayor detalle y cuidado posible los casos que sí tenés. Sin embargo, los estudios de caso también tienen ventajas genuinas: como no tenés tantas personas para estudiar, podés invertir mucho más tiempo y esfuerzo en tratar de entender los factores específicos en juego en cada caso. Y eso es algo muy valioso. Como consecuencia, los estudios de caso pueden complementar los enfoques más estadísticos que ves en los diseños experimentales y cuasi-experimentales. No vamos a hablar mucho de estudios de caso en estas clases, ¡pero siguen siendo herramientas muy valiosas!

1.11 Evaluar la validez de un estudio

Más que cualquier otra cosa, un científico quiere que su investigación sea “válida”. La idea conceptual detrás de la validez es muy simple: ¿podés confiar en los resultados de tu estudio? Si no, el estudio es inválido. Sin embargo, aunque es fácil de enunciar, en la práctica es mucho más difícil verificar la validez que la confiabilidad. Y para ser sinceros, no hay una noción precisa y universalmente aceptada de qué es la validez. De hecho, existen muchos tipos diferentes de validez, cada una con sus propios problemas, y no todas son relevantes para todos los estudios. Voy a hablar de cinco tipos diferentes:

• Validez interna
  
• Validez externa
  
• Validez de constructo
  
• Validez aparente
  
• Validez ecológica

Para darte una guía rápida de lo que importa acá… (1) La validez interna y externa son las más importantes, ya que están directamente relacionadas con la pregunta fundamental de si tu estudio realmente funciona. (2) La validez de constructo pregunta si estás midiendo lo que creés que estás midiendo. (3) La validez aparente no es especialmente importante, excepto en la medida en que te preocupen las “apariencias”. (4) La validez ecológica es un caso especial de validez aparente que se refiere a un tipo de apariencia que puede importarte bastante.

1.11.1 Validez interna

La validez interna se refiere al grado en que podés sacar conclusiones correctas sobre las relaciones causales entre variables. Se llama “interna” porque refiere a las relaciones entre cosas “dentro” del estudio. Vamos a ilustrar este concepto con un ejemplo simple. Supongamos que te interesa saber si una educación universitaria mejora la escritura. Para eso, reunís un grupo de estudiantes de primer año, les pedís que escriban un ensayo de 1000 palabras, y contás los errores ortográficos y gramaticales. Luego hacés lo mismo con estudiantes de tercer año, que obviamente tienen más educación universitaria que los de primer año. Y supongamos que los de tercer año cometen menos errores. Entonces concluís que la educación universitaria mejora las habilidades de escritura. ¿No? El gran problema de este experimento es que los estudiantes de tercer año son mayores y tienen más experiencia escribiendo. Así que no es fácil saber cuál es la relación causal real: ¿las personas mayores escriben mejor? ¿O las personas con más experiencia escribiendo? ¿O las personas con más educación? ¿Cuál de estas es la verdadera causa del mejor desempeño de los de tercer año? ¿La edad? ¿La experiencia? ¿La educación? No lo podés saber. Este es un ejemplo de una falla de validez interna, porque tu estudio no permite desentrañar bien las relaciones causales entre las variables.

1.11.2 Validez externa

La validez externa se refiere a la generalización de tus resultados. Es decir, hasta qué punto esperás ver el mismo patrón de resultados en la “vida real” que el que observaste en tu estudio. Más precisamente, cualquier estudio que hagas en psicología va a involucrar un conjunto bastante específico de preguntas o tareas, va a ocurrir en un entorno específico y va a incluir participantes de un subgrupo particular. Entonces, si resulta que los resultados no se generalizan a personas o situaciones fuera de las que estudiaste, entonces tenés un problema de validez externa.

El ejemplo clásico de este problema es el hecho de que una gran proporción de los estudios en psicología usan estudiantes universitarios de psicología como participantes. Pero claramente, a los investigadores no les interesa solo ese grupo: les interesa la gente en general. Dado eso, un estudio que solo incluye estudiantes de psicología como participantes siempre corre el riesgo de carecer de validez externa. Es decir, si hay algo “especial” en los estudiantes de psicología que los hace diferentes de la población general en algún aspecto relevante, entonces podríamos preocuparnos por la validez externa.

Dicho esto, es absolutamente crucial darse cuenta de que un estudio que incluye únicamente estudiantes de psicología no necesariamente tiene un problema de validez externa. Lo voy a mencionar más adelante, pero como es un error muy común, lo digo ya: la validez externa se ve amenazada por la elección de población si (a) la población de la que tomaste tu muestra es muy limitada (por ejemplo, estudiantes de psicología) y (b) esa población limitada es sistemáticamente diferente de la población general en algún aspecto relevante para el fenómeno psicológico que querés estudiar. Esa parte en cursiva es la que muchos olvidan: es cierto que los estudiantes de psicología difieren de la población general en muchas cosas, así que un estudio que solo incluye estudiantes puede tener problemas de validez externa. Pero si esas diferencias no son relevantes para el fenómeno que estás estudiando, entonces no hay de qué preocuparse. Para hacerlo más concreto, acá van dos ejemplos extremos:

• Querés medir “las actitudes del público general hacia la psicoterapia”, pero todos tus participantes son estudiantes de psicología. Este estudio casi con certeza tendría problemas de validez externa.

• Querés medir la efectividad de una ilusión visual, y todos tus participantes son estudiantes de psicología. Este estudio muy probablemente no tendría problemas de validez externa.

Después de haberme centrado varios párrafos en la elección de participantes (porque es el tema que más preocupa a todos), vale la pena recordar que la validez externa es un concepto más amplio. Los siguientes también son ejemplos de cosas que pueden amenazar la validez externa, según qué tipo de estudio estés haciendo:

• Puede que la gente responda un “cuestionario de psicología” de un modo que no refleja cómo actuaría en la vida real.

• Tu experimento de laboratorio sobre “aprendizaje humano” podría tener una estructura diferente de los problemas de aprendizaje que la gente enfrenta fuera del laboratorio.

1.11.3 Validez de constructo

La validez de constructo es, básicamente, la pregunta de si estás midiendo lo que realmente querés medir. Una medición tiene buena validez de constructo si realmente mide el constructo teórico correcto, y mala validez de constructo si no lo hace. Para dar un ejemplo muy simple (aunque ridículo), supongamos que quiero investigar qué porcentaje de estudiantes universitarios hacen trampa en los exámenes. Y la manera en que intento medirlo es pidiéndoles a los estudiantes que hacen trampa que se paren en el aula para que pueda contarlos. Cuando hago esto en una clase de 300 estudiantes, nadie se levanta. Entonces concluyo que el porcentaje de estudiantes que hacen trampa es 0%. Claramente esto es ridículo. Pero el punto acá no es que sea un gran ejemplo metodológico, sino que ilustra qué es la validez de constructo. El problema con mi medición es que aunque intento medir “el porcentaje de personas que hacen trampa”, lo que en realidad estoy midiendo es “el porcentaje de personas lo suficientemente tontas como para admitirlo, o lo suficientemente provocadoras como para fingir que lo hacen”. Obviamente, ¡eso no es lo mismo! Así que mi estudio sale mal porque mi medición tiene una validez de constructo muy pobre.

1.11.4 Validez aparente

La validez aparente simplemente se refiere a si una medición “parece” estar haciendo lo que se supone que hace, y nada más. Si diseño un test de inteligencia, y la gente lo mira y dice “no, ese test no mide inteligencia”, entonces mi medición carece de validez aparente. Así de simple. Obviamente, la validez aparente no es muy importante desde una perspectiva científica pura. Después de todo, lo que nos importa es si la medición realmente hace lo que se supone que haga, no si parece hacerlo. Como consecuencia, generalmente no nos preocupa demasiado la validez aparente. Dicho esto, el concepto tiene tres usos pragmáticos útiles:

• A veces, un científico con experiencia tiene la “intuición” de que una medición no va a funcionar. Aunque esas intuiciones no tienen valor como evidencia en sí mismas, suele valer la pena prestarles atención. Porque muchas veces las personas tienen conocimientos que no pueden verbalizar del todo, puede haber algo preocupante incluso si no puedes explicar bien qué. En otras palabras, si alguien en quien confiás critica la validez aparente de tu estudio, conviene tomarse el tiempo de revisar bien el diseño para ver si encontrás razones por las que podría fallar. Ahora bien, si no encontrás nada, entonces probablemente no haya motivo para preocuparse: al fin y al cabo, la validez aparente no es muy relevante.

• Muchas veces (muchísimas), personas completamente desinformadas también tienen la “intuición” de que tu investigación es mala. Y la van a criticar en internet o donde sea. Si mirás de cerca, vas a notar que muchas de esas críticas están centradas únicamente en cómo “luce” el estudio, pero no en nada más profundo. El concepto de validez aparente sirve para explicarles amablemente que necesitan fundamentar mejor sus argumentos.

• En relación con lo anterior: si las creencias de personas sin formación científica son clave (por ejemplo, en investigación aplicada donde querés convencer a responsables de políticas), entonces tenés que preocuparte por la validez aparente. Simplemente porque —te guste o no— mucha gente va a usar la validez aparente como sustituto de la validez real. Si querés que el gobierno cambie una ley con base en datos científicos o psicológicos, no va a importar cuán buenos sean realmente tus estudios. Si carecen de validez aparente, los políticos te van a ignorar. Claro que es algo injusto que las políticas dependan más de las apariencias que en hechos, pero así funcionan las cosas.

1.11.5 Validez ecológica

La validez ecológica es una noción diferente de validez, parecida a la validez externa, pero menos importante. La idea es que, para que un estudio sea ecológicamente válido, toda su configuración debería parecerse mucho al escenario real que se está investigando. En cierto sentido, la validez ecológica es un tipo de validez aparente –refiere principalmente a si el estudio “luce” correcto, pero con un poco más de rigor. Para que tenga validez ecológica, el estudio tiene que parecer correcto de una manera bastante específica. La idea que la sustenta es la intuición de que un estudio con validez ecológica tiene más probabilidades de tener validez externa. No es una garantía, claro. Pero lo bueno de la validez ecológica es que es mucho más fácil de evaluar que la validez externa. Un ejemplo simple serían los estudios de identificación de testigos. Muchos de estos estudios suelen hacerse en entornos universitarios, a menudo con una disposición bastante simple de rostros para observar, en lugar de una rueda de reconocimiento real. El tiempo entre ver al “criminal” y que se le pida a la persona que lo identifique en la “rueda” suele ser más corto. El “crimen” no es real, así que no hay posibilidad de que el testigo esté asustado, y no hay policías presentes, así que hay menos probabilidad de que sientan presión. Todo eso significa que el estudio definitivamente carece de validez ecológica. Tal vez (o tal vez no) también carezca de validez externa.

1.12 Confusores, artefactos y otras amenazas a la validez

Si consideramos el tema de la validez en términos generales, las dos grandes preocupaciones que tenemos son los confusores y los artefactos. Estos dos términos se definen de la siguiente manera:

• Confusor: Un confusor es una variable adicional, a menudo no medida, que resulta estar relacionada tanto con las variables predictoras como con los resultados. La existencia de confusores amenaza la validez interna del estudio, porque no podés saber si la variable predictora causa el resultado, o si lo causa la variable confusora, etc.

• Artefacto: Se dice que un resultado es “artefactual” si solo se sostiene en la situación especial que se usó para hacer el estudio. La posibilidad de que tu resultado sea un artefacto representa una amenaza a la validez externa, porque plantea la posibilidad de que no puedas generalizar tus resultados a la población real que te interesa.

Como regla general, los confusores son una preocupación mayor en los estudios no experimentales, precisamente porque no son experimentos propiamente dichos: por definición, estás dejando muchas cosas sin controlar, así que hay mucho margen para que los confusores se metan en tu estudio. La investigación experimental tiende a ser mucho menos vulnerable a los confusores: cuanto más control tenés sobre lo que ocurre durante el estudio, más podés evitar que aparezcan confusores.

Sin embargo, una de cal y otra de arena: cuando empezamos a pensar en artefactos en lugar de confusores, la situación se invierte por completo. En general, los resultados artefactuales tienden a ser una preocupación mayor en los estudios experimentales que en los no experimentales. Para ver esto, ayuda entender que muchas veces los estudios son no experimentales precisamente porque la persona investigadora quiere examinar el comportamiento humano en un contexto más naturalista. Al trabajar en un contexto más cercano al mundo real, perdés control experimental (lo que te hace vulnerable a confusores), pero como tendés a estudiar la psicología humana “en estado salvaje”, reducís las probabilidades de obtener un resultado artefactual. O, dicho de otra manera, cuando sacás la psicología del entorno natural y la llevás al laboratorio (lo que normalmente tenemos que hacer para ganar control experimental), siempre corrés el riesgo de terminar estudiando algo diferente de lo que realmente querías estudiar: lo cual es, más o menos, la definición de un artefacto.

Advertencia: lo anterior es solo una guía general. Es totalmente posible que haya confusores en un experimento, y también obtener resultados artefactuales en estudios no experimentales. Esto puede pasar por muchas razones, entre ellas, errores de la persona investigadora. En la práctica, es realmente difícil prever todo por adelantado, y hasta los investigadores más competentes cometen errores. Pero otras veces es inevitable, simplemente porque la persona investigadora tiene ética (por ejemplo, ver “abandono diferencial”).

Bien. En cierto sentido, casi cualquier amenaza a la validez puede caracterizarse como un confusor o un artefacto: son conceptos bastante vagos. Así que veamos algunos de los ejemplos más comunes…

1.12.1 Efectos de historia

Los efectos de historia se refieren a la posibilidad de que ocurran eventos específicos durante el desarrollo del estudio que puedan influir en los resultados. Por ejemplo, algo podría pasar entre una medición pretest y una postest. O entre los participantes 23 y 24. Alternativamente, puede ser que estés revisando un estudio antiguo, que era perfectamente válido en su momento, pero el mundo ha cambiado lo suficiente desde entonces como para que sus conclusiones ya no sean confiables. Algunos ejemplos de lo que contarían como efectos de historia:

• Estás interesado en cómo la gente piensa sobre el riesgo y la incertidumbre. Comenzás a recolectar datos en diciembre de 2010. Pero encontrar participantes y juntar datos lleva tiempo, así que seguís trabajando en eso durante febrero de 2011. Lamentablemente para vos (y aún más lamentablemente para otros), las inundaciones en Queensland ocurrieron en enero de 2011, causando miles de millones de dólares en daños y matando a muchas personas. No sorprende que las personas evaluadas en febrero de 2011 expresen creencias bastante distintas sobre cómo manejar el riesgo que aquellas evaluadas en diciembre de 2010. ¿Cuál (si alguna) de estas refleja las creencias “verdaderas” de los participantes? Creo que la respuesta probablemente sea ambas: las inundaciones en Queensland cambiaron genuinamente las creencias del público australiano, aunque tal vez solo temporalmente. Lo importante acá es que la “historia” de las personas evaluadas en febrero es bastante distinta de la de quienes fueron evaluades en diciembre.

• Estás evaluando los efectos psicológicos de una nueva droga contra la ansiedad. Entonces lo que hacés es medir la ansiedad antes de administrar la droga (por ejemplo, mediante autoinforme y medidas fisiológicas, digamos), luego administrás la droga, y después volvés a tomar las mismas medidas. Sin embargo, en el medio, como tu laboratorio está en Los Ángeles, ocurre un terremoto, lo cual incrementa la ansiedad de los participantes.

1.12.2 Efectos de maduración

Al igual que los efectos de historia, los efectos de maduración están fundamentalmente relacionados con el cambio a lo largo del tiempo. Sin embargo, los efectos de maduración no son una respuesta a eventos específicos. Más bien, tienen que ver con cómo cambian las personas por sí solas con el paso del tiempo: envejecemos, nos cansamos, nos aburrimos, etc. Algunos ejemplos de efectos de maduración:

• Cuando hacés investigación en psicología del desarrollo, necesitás tener en cuenta que los niños crecen bastante rápido. Supongamos que querés averiguar si cierta estrategia educativa ayuda a aumentar el vocabulario en niños de 3 años. Algo que necesitás considerar es que el tamaño del vocabulario en niños de esa edad está creciendo a un ritmo increíble (varias palabras por día), por sí solo. Si diseñás tu estudio sin tener en cuenta este efecto de maduración, entonces no vas a poder saber si tu estrategia educativa realmente funciona.

• Cuando realizás un experimento muy largo en el laboratorio (digamos, algo que dura 3 horas), es muy probable que las personas empiecen a aburrirse y a cansarse, y que ese efecto de maduración va a causar una disminución en el rendimiento, independientemente de cualquier otra cosa que esté pasando en el experimento.

1.12.3 Efectos de pruebas repetidas

Un tipo importante de efecto de historia es el efecto de las pruebas repetidas. Supongamos que quiero tomar dos mediciones de algún constructo psicológico (por ejemplo, ansiedad). Algo que podría preocuparme es si la primera medición afecta la segunda. En otras palabras, este es un efecto de historia en el que el “evento” que influye sobre la segunda medición es ¡la primera medición en sí misma! Esto no es nada raro. Algunos ejemplos de esto incluyen:

• Aprendizaje y práctica: por ejemplo, la “inteligencia” en el tiempo 2 podría parecer más alta que en el tiempo 1 porque los participantes aprendieron las reglas generales para resolver preguntas “tipo test de inteligencia” durante la primera sesión.

• Familiaridad con la situación de evaluación: por ejemplo, si las personas están nerviosas en el tiempo 1, eso podría hacer que su rendimiento baje; después de atravesar la primera sesión, podrían calmarse precisamente porque ya vieron cómo es la situación de evaluación.

• Cambios auxiliares causados por la evaluación: por ejemplo, si un cuestionario para medir el estado de ánimo es aburrido, entonces el estado de ánimo medido en el tiempo 2 probablemente sea “aburrido”, justamente por haber pasado por una evaluación aburrida en el tiempo 1.

1.12.4 Sesgo de selección

El sesgo de selección es un término bastante amplio. Supongamos que estás llevando a cabo un experimento con dos grupos de participantes, donde cada grupo recibe un “tratamiento” diferente, y querés ver si esos tratamientos generan distintos resultados. Sin embargo, supongamos que, a pesar de tus mejores esfuerzos, terminás con un desequilibrio de género entre los grupos (por ejemplo, el grupo A tiene 80% mujeres y el grupo B tiene 50%). Puede sonar como algo que nunca pasaría, pero creeme, pasa. Este es un ejemplo de sesgo de selección, en el cual las personas que fueron asignadas a los dos grupos tienen características distintas. Si resulta que alguna de esas características es relevante (por ejemplo, que tu tratamiento funciona mejor para mujeres que para varones), entonces estás en serios problemas.

1.12.5 Abandono diferencial

Un peligro bastante sutil al que hay que prestarle atención se llama abandono diferencial, que es un tipo de sesgo de selección causado por el propio estudio. Supongamos que, por primera vez en la historia de la psicología, logro encontrar una muestra perfectamente balanceada y representativa de personas. Empiezo a correr “el experimento increíblemente largo y tedioso de Dan” sobre mi muestra perfecta, pero como mi estudio es increíblemente largo y tedioso, mucha gente empieza a abandonar. No puedo evitarlo: como vamos a discutir más adelante en el capítulo sobre ética en la investigación, los participantes tienen absolutamente el derecho de dejar cualquier experimento, en cualquier momento, por la razón que se les ocurra, y como investigadores tenemos la obligación moral (y profesional) de recordarles que tienen ese derecho. Entonces, supongamos que “el experimento increíblemente largo y tedioso de Dan” tiene una tasa de abandono muy alta. ¿Qué probabilidades creés que hay de que ese abandono sea aleatorio? Respuesta: cero. Casi con certeza, las personas que permanecen son más concienzudas, más tolerantes al aburrimiento, etc., que aquellas que se van. En la medida en que (por ejemplo) la concienzudez sea relevante para el fenómeno psicológico que me interesa, este abandono puede disminuir la validez de mis resultados.

Cuando se piensa en los efectos del abandono diferencial, a veces resulta útil distinguir entre dos tipos diferentes. El primero es el abandono homogéneo, en el que el efecto del abandono es el mismo para todos los grupos, tratamientos o condiciones. En el ejemplo que di más arriba, el abandono diferencial sería homogéneo si (y solo si) los participantes que se aburren fácilmente están abandonando todas las condiciones del experimento más o menos al mismo ritmo. En general, el principal efecto del abandono homogéneo es que puede volver tu muestra no representativa. En ese caso, la principal preocupación es que la generalización de los resultados disminuye: en otras palabras perdés validez externa.

El segundo tipo de abandono diferencial es el abandono heterogéneo, en el que el efecto del abandono es distinto para diferentes grupos. Este es un problema mucho más grave: no solo tenés que preocuparte por tu validez externa, sino también por tu validez interna. Para ver por qué es así, consideremos un estudio muy tonto en el que quiero ver si insultar a las personas hace que actúen de manera más obediente. No sé por qué alguien querría estudiar eso, pero supongamos que a mí me importa muchísimo. Entonces, diseño mi experimento con dos condiciones. En la condición de “tratamiento”, la persona experimentadora insulta a la persona participante y luego le da un cuestionario diseñado para medir obediencia. En la condición de “control”, la persona experimentadora conversa un poco sin decir nada importante y luego le da el mismo cuestionario. Dejando de lado los dudosos méritos científicos y éticos de tal estudio, pensemos qué podría salir mal acá. Como regla general, cuando alguien me insulta en la cara, tiendo a volverme mucho menos cooperativo. Así que hay una buena probabilidad de que muchas más personas abandonen la condición de tratamiento que la condición de control. Y ese abandono no va a ser aleatorio. Las personas más propensas a abandonar probablemente sean aquellas a las que no les importa tanto la importancia de quedarse obedientemente en el experimento. Como las personas más testarudas y desobedientes se fueron del grupo de tratamiento pero no del grupo de control, hemos introducido un confusor: las personas que efectivamente completaron el cuestionario en el grupo de tratamiento ya eran más propensas a ser obedientes y cumplidoras que las del grupo de control. En resumen, en este estudio insultar a la gente no la vuelve más obediente: ¡hace que los más desobedientes se vayan del experimento! La validez interna de este experimento queda completamente arruinada.

1.12.6 Sesgo por no respuesta

El sesgo por no respuesta está estrechamente relacionado con el sesgo de selección y con el abandono diferencial. La versión más simple del problema va así: enviás una encuesta por correo a 1000 personas, y solo 300 responden. Las 300 personas que respondieron casi con seguridad no son una submuestra aleatoria. Las personas que responden encuestas son sistemáticamente diferentes de las que no lo hacen. Esto genera un problema cuando intentás generalizar a partir de esas 300 personas que sí respondieron hacia toda la población, ya que ahora tenés una muestra muy poco aleatoria.

Sin embargo, el problema del sesgo por no respuesta es más general que eso. Entre las (digamos) 300 personas que respondieron la encuesta, podrías encontrar que no todas contestan todas las preguntas. Si (por ejemplo) 80 personas eligieron no responder una de tus preguntas, ¿eso introduce problemas? Como siempre, la respuesta es: tal vez. Si la pregunta que no se respondió estaba en la última página del cuestionario, y esas 80 encuestas fueron devueltas sin la última página, hay una buena probabilidad de que esos datos faltantes no sean un gran problema: probablemente las páginas simplemente se desprendieron. Sin embargo, si la pregunta que 80 personas no respondieron era la más confrontativa o invasiva del cuestionario, entonces casi con certeza tenés un problema. En esencia, lo que estás enfrentando acá es lo que se llama el problema de datos faltantes. Si los datos que faltan se “perdieron” de manera aleatoria, entonces no es un gran problema. Si faltan de forma sistemática, entonces sí puede ser un gran problema.

1.12.7 Regresión a la media

La regresión a la media es una curiosa variación del sesgo de selección. Se refiere a cualquier situación en la que seleccionás datos basándote en un valor extremo de alguna medición. Debido a la variación natural de la medición, eso casi con certeza significa que, cuando tomes una segunda medición, ese nuevo valor será menos extremo que el primero, simplemente por azar.

Acá va un ejemplo. Supongamos que me interesa saber si una formación en psicología tiene un efecto negativo en los estudiantes muy inteligentes. Para esto, busco a los 20 estudiantes de psicología con las mejores calificaciones del secundario y analizo qué tan bien les va en la universidad. Resulta que les va mucho mejor que el promedio, pero no están encabezando la clase en la universidad, aunque sí lo hacían en el secundario. ¿Qué está pasando? El primer pensamiento natural es que esto debe significar que las clases de psicología están teniendo un efecto negativo sobre esos estudiantes. Sin embargo, aunque esa podría ser la explicación, lo más probable es que lo que estás viendo sea un ejemplo de “regresión a la media”. Para entender cómo funciona, tomémonos un momento para pensar qué se necesita para obtener la mejor nota en una clase, ya sea en el secundario o en la universidad. Cuando tenés una clase grande, va a haber muchas personas muy inteligentes. Para sacar la mejor nota tenés que ser muy inteligente, trabajar muy duro, y tener un poco de suerte. El examen tiene que hacer exactamente las preguntas correctas para tus habilidades particulares, y no tenés que cometer errores tontos (que todos cometemos alguna vez) al responderlas. Y ese es el punto: la inteligencia y el esfuerzo son cualidades que se transfieren de una clase a otra. La suerte, no. Los que tuvieron suerte en el secundario no van a ser los mismos que tienen suerte en la universidad. Esa es, justamente, la definición de “suerte”. Como consecuencia, cuando seleccionás personas con valores muy extremos en una medición (los 20 mejores estudiantes), estás seleccionando por esfuerzo, habilidad y suerte. Pero como la suerte no se transfiere a la segunda medición (solo la habilidad y el esfuerzo sí lo hacen), es de esperar que todos esos estudiantes bajen un poco cuando los medís por segunda vez (en la universidad). Así que sus calificaciones caen un poco, se acercan de nuevo al resto. Eso es la regresión a la media.

La regresión a la media es sorprendentemente común. Por ejemplo, si dos personas muy altas tienen hijos, sus hijos tenderán a ser más altos que el promedio, pero no tanto como sus padres. Lo inverso ocurre con padres muy bajos: dos padres muy bajos tenderán a tener hijos bajos, pero aún así esos hijos tenderán a ser más altos que sus padres. También puede ser extremadamente sutil. Por ejemplo, se han hecho estudios que sugerían que las personas aprenden mejor del feedback negativo que del positivo. Sin embargo, la forma en que se trató de demostrar esto fue dando refuerzo positivo cuando los participantes lo hacían bien, y refuerzo negativo cuando lo hacían mal. Y lo que se observa es que después del refuerzo positivo, el desempeño tendía a empeorar; pero después del refuerzo negativo, tendía a mejorar. ¡Pero! Fijate que acá hay un sesgo de selección: cuando las personas lo hacen muy bien, estás seleccionando valores “altos”, y por lo tanto deberías esperar (por la regresión a la media) que el rendimiento en la siguiente prueba sea peor, independientemente de si se da refuerzo o no. De manera similar, después de una mala prueba, la gente tenderá a mejorar por sí sola. La aparente superioridad del feedback negativo es un artefacto causado por la regresión a la media (Kahneman y Tversky 1973).

1.12.8 Sesgo del experimentador

El sesgo del experimentador puede presentarse de múltiples formas. La idea básica es que la persona experimentadora, a pesar de tener las mejores intenciones, puede terminar influyendo accidentalmente en los resultados del experimento al comunicar sutilmente la “respuesta correcta” o el “comportamiento deseado” a los participantes. Típicamente, esto ocurre porque la persona experimentadora posee un conocimiento especial que la persona participante no tiene —ya sea la respuesta correcta a las preguntas que se hacen, o el patrón de desempeño esperado para la condición en la que se encuentra la persona participante, etc. El ejemplo clásico de esto es el estudio de caso de “Hans el listo”, que data de 1907 (Pfungst 1911; Hothersall 2004). Hans el listo era un caballo que aparentemente podía leer, contar y realizar otras hazañas de inteligencia típicamente humanas. Después de que Hans se hizo famoso, los psicólogos comenzaron a examinar más de cerca su comportamiento. Resultó que —como era de esperarse— Hans no sabía hacer cuentas. En realidad, Hans estaba respondiendo a los observadores humanos a su alrededor. Como ellos sí sabían contar, el caballo había aprendido a cambiar su comportamiento cuando los humanos cambiaban el suyo.

La solución general al problema del sesgo del experimentador es realizar estudios doble ciego, en los que ni la persona experimentadora ni la persona participante saben en qué condición se encuentra la persona participante, ni cuál es el comportamiento deseado. Esta es una muy buena solución al problema, pero es importante reconocer que no es del todo ideal y que es difícil implementarla perfectamente.

Por ejemplo, la manera obvia en que podría intentar construir un estudio doble ciego es pedirle a uno de mis estudiantes de doctorado (alguien que no sepa nada sobre el experimento) que lleve a cabo el estudio. Eso parecería suficiente. La única persona (yo) que conoce todos los detalles (por ejemplo, las respuestas correctas a las preguntas, la asignación de participantes a condiciones) no interactúa con los participantes, y la persona que sí habla con ellos (el estudiante de doctorado) no sabe nada.

Salvo que, esa última parte es muy poco probable que sea cierta. Para que el estudiante de doctorado pueda llevar a cabo el estudio de manera efectiva, tiene que haber recibido instrucciones mías, la persona investigadora. Y, como ocurre, ese estudiante también me conoce, y sabe un poco sobre mis creencias generales acerca de las personas y la psicología (por ejemplo, tiendo a pensar que los seres humanos son mucho más inteligentes de lo que los psicólogos reconocen). Como resultado de todo esto, es casi imposible que la persona experimentadora evite conocer, aunque sea un poco, mis expectativas. Y hasta un poco de conocimiento puede tener efecto: supongamos que la persona experimentadora transmite accidentalmente el hecho de que se espera que los participantes lo hagan bien en esta tarea. Bueno, hay algo que se llama el “efecto Pigmalión”: si esperás grandes cosas de alguien, esa persona tenderá a estar a la altura; pero si esperás que fracase, probablemente lo haga. En otras palabras, las expectativas se vuelven profecías autocumplidas.

1.12.9 Efectos de demanda y reactividad

Cuando hablamos del sesgo del experimentador, la preocupación es que el conocimiento o los deseos de la persona experimentadora respecto al experimento se comuniquen a los participantes, y que eso afecte su comportamiento (Rosenthal 1966). Sin embargo, incluso si lográs evitar que eso ocurra, es casi imposible evitar que los participantes sepan que están participando en un estudio psicológico. Y el mero hecho de saber que alguien te está observando o estudiando puede tener un efecto bastante fuerte sobre el comportamiento. A esto se lo denomina en general como reactividad o efectos de demanda. La idea básica se captura en el efecto Hawthorne: las personas modifican su rendimiento debido a la atención que el estudio pone sobre elles. El efecto toma su nombre de la fábrica “Hawthorne Works” en las afueras de Chicago (Adair 1984). Un estudio hecho en la década de 1920 que examinaba los efectos de la iluminación sobre la productividad de los trabajadores en la fábrica resultó mostrar un efecto del hecho de que los trabajadores sabían que estaban siendo estudiados, más que de la iluminación.

Para ser un poco más específicos sobre algunas de las formas en que el solo hecho de estar en un estudio puede cambiar cómo actúan las personas, ayuda pensar como un psicólogo social y observar algunos de los roles que las personas podrían adoptar durante un experimento, pero que tal vez no adoptarían si los mismos eventos ocurrieran en el mundo real:

• La persona participante colaboradora intenta ser demasiado útil para la persona investigadora: busca entender la hipótesis y confirmarla.

• La persona participante negativa hace exactamente lo opuesto a la colaboradora: busca sabotear o destruir el estudio o la hipótesis de alguna manera.

• La persona participante fiel es antinaturalmente obediente: busca seguir las instrucciones a la perfección, sin importar lo que hubiera sucedido en una situación más realista.

• La persona participante aprensiva se pone nerviosa por estar siendo evaluada o estudiada, tanto que su comportamiento se vuelve altamente antinatural o excesivamente deseable socialmente.

1.12.10 Efectos placebo

El efecto placebo es un tipo específico de efecto de demanda que nos preocupa bastante. Se refiere a la situación en la que el simple hecho de recibir un tratamiento provoca una mejora en los resultados. El ejemplo clásico proviene de los ensayos clínicos: si le das a una persona un fármaco completamente inerte desde el punto de vista químico y le decís que es una cura para una enfermedad, esa persona tiende a mejorar más rápido que alguien que no recibe ningún tratamiento. En otras palabras, es la creencia de que están recibiendo tratamiento lo que causa la mejora, no el medicamento en sí.

1.12.11 Efectos de situación, medición y subpoblación

En algunos aspectos, estos términos funcionan como una categoría general para “todas las demás amenazas a la validez externa”. Se refieren al hecho de que la elección de la subpoblación de la que obtenés a tus participantes, la ubicación, el momento y la manera en que llevás a cabo tu estudio (incluyendo quién recolecta los datos), y las herramientas que usás para hacer tus mediciones podrían estar influyendo en los resultados. En concreto, la preocupación es que estas cosas puedan estar influyendo en los resultados de una manera tal que impida generalizar a una gama más amplia de personas, contextos y métodos de medición.

1.12.12 Fraude, engaño y autoengaño

Es difícil lograr que alguien entienda algo, cuando su salario depende de que no lo entienda.
— Upton Sinclair

Una última cosa que siento que debería mencionar. Mientras leía lo que suelen decir los libros de texto sobre cómo evaluar la validez de un estudio, no pude evitar notar que parecen asumir que la persona investigadora es honesta. Me resulta gracioso. Aunque la gran mayoría de los científicos son honestos —al menos en mi experiencia—, algunos no lo son. No solo eso: como mencioné antes, los científicos no son inmunes al sesgo de creencias —es fácil que un investigador termine engañándose a sí misme para creer algo falso, y eso puede llevarle a hacer investigaciones sutilmente defectuosas, y luego a ocultar esas fallas al redactar el informe. Así que necesitás considerar no solo la (probablemente poco común) posibilidad de fraude deliberado, sino también la (probablemente bastante común) posibilidad de que la investigación esté sesgada de manera no intencional. Abrí algunos libros de texto estándar y no encontré mucho sobre este problema, así que acá va mi propio intento de listar algunas formas en que pueden surgir estas cuestiones:

• Fabricación de datos. A veces, las personas simplemente inventan los datos. Ocasionalmente esto se hace con “buenas” intenciones. Por ejemplo, la persona investigadora cree que los datos fabricados reflejan la verdad, y pueden ser versiones “ligeramente corregidas” de datos reales. En otras ocasiones, el fraude es deliberado y malicioso. Algunos ejemplos de alto perfil en los que se ha alegado o demostrado fabricación de datos incluyen a Cyril Burt (un psicólogo que se cree que falsificó parte de sus datos), Andrew Wakefield (acusado de falsificar sus datos que relacionaban la vacuna triple viral con el autismo) y Hwang Woo-suk (quien falsificó muchos de sus datos sobre investigación con células madre).

• Engaños (hoaxes). Los engaños comparten muchas similitudes con la fabricación de datos, pero se diferencian en el propósito. Un engaño suele ser una broma, y muchos están diseñados para que (eventualmente) se descubran. A menudo, el objetivo de un engaño es desacreditar a alguien o a un campo entero. Ha habido bastantes engaños científicos conocidos a lo largo de los años (por ejemplo, el hombre de Piltdown), algunos de los cuales fueron intentos deliberados de desacreditar ciertos campos de investigación (por ejemplo, el caso Sokal).

• Falsificación o tergiversación de los datos. Aunque el fraude es lo que se lleva los titulares, en mi experiencia es mucho más común ver datos tergiversados. Cuando digo esto, no me refiero a los medios de comunicación interpretando mal los resultados (lo cual hacen casi siempre). Me refiero a que muchas veces los datos no dicen realmente lo que los investigadores creen que dicen. Mi impresión es que, casi siempre, esto no se debe a una deshonestidad deliberada, sino a una falta de sofisticación en los análisis de datos. Por ejemplo, pensá en el caso de la paradoja de Simpson que mencioné al comienzo de estas notas. Es muy común ver a personas presentar datos “agregados” de algún tipo; y a veces, cuando profundizás y conseguís los datos crudos por tu cuenta, encontrás que los datos agregados cuentan una historia diferente que los desagregados. Alternativamente, podrías descubrir que algún aspecto de los datos está siendo ocultado porque cuenta una historia incómoda (por ejemplo, la persona investigadora podría optar por no mencionar una determinada variable). Hay muchas variantes de esto; muchas de las cuales son muy difíciles de detectar.

• Diseño “defectuoso” del estudio. Bien, esto es más sutil. Básicamente, el problema acá es que un investigador diseña un estudio que tiene fallas estructurales, y esas fallas nunca se informan en el artículo. Los datos que se reportan son completamente reales, y están analizados correctamente, pero provienen de un estudio que en realidad está muy mal planteado. La persona investigadora realmente quiere encontrar un efecto en particular, así que el estudio se arma de manera tal que resulte “fácil” (aunque artefactual) observar ese efecto. Una manera muy astuta de hacer esto —por si tenés ganas de incursionar en un poco de fraude— es diseñar un experimento en el que sea obvio para los participantes qué es lo que “se supone” que deben hacer, y luego dejar que la reactividad haga su magia. Si querés, podés agregarle todos los adornos de un experimento doble ciego, etc. No va a hacer ninguna diferencia, ya que los propios materiales del estudio les están diciendo sutilmente a los participantes lo que se espera que hagan. Cuando redactás los resultados, el fraude no va a ser obvio para la persona lectora: lo que es evidente para la persona participante en el contexto experimental no siempre es evidente para quien lee el artículo. Claro, la manera en que describí esto suena como si siempre fuera fraude: probablemente haya casos donde esto se haga de forma deliberada, pero en mi experiencia la preocupación más grande ha sido con los errores no intencionales de diseño. La persona investigadora cree… y así, el estudio termina teniendo una falla estructural, y esa falla mágicamente desaparece cuando se escribe el artículo para su publicación.

• Minería de datos e hipótesis post hoc. Otra forma en la que los autores de un estudio pueden, más o menos, mentir sobre lo que encontraron es mediante lo que se llama “minería de datos”. Como vamos a discutir más adelante en la clase, si analizás los datos de muchas formas diferentes, eventualmente vas a encontrar algo que “parece” un efecto real, pero que no lo es. Eso es lo que se llama “minería de datos”. Antes era bastante raro, porque analizar datos solía llevar semanas, pero ahora que todos tienen software estadístico muy potente en sus computadoras, se ha vuelto bastante común. La minería de datos en sí no es “incorrecta”, pero cuanto más la hacés, más grande es el riesgo que estás corriendo. Lo que sí está mal (y, sospecho, es común) es hacer minería de datos sin reconocerlo. Es decir, la persona investigadora prueba todos los análisis posibles conocidos por la humanidad, encuentra uno que “funciona”, y luego finge que ese era el único análisis que pensaba hacer desde el principio. Peor aún, muchas veces “inventa” una hipótesis después de mirar los datos, para cubrir la minería de datos. Para ser claros: no está mal cambiar tus creencias después de mirar los datos, y reanalizar los datos con tus nuevas hipótesis post hoc. Lo que sí está mal (y, sospecho, es común) es no reconocer que hiciste eso. Si lo reconocés, otros investigadores pueden tenerlo en cuenta. Si no lo hacés, no pueden. Y eso vuelve tu comportamiento engañoso. ¡Mal!

• Sesgo de publicación y autocensura. Finalmente, un sesgo muy extendido es el de la no publicación de resultados negativos. Y esto es casi imposible de evitar. Las revistas científicas no publican todo lo que se les envía: tienden a preferir los artículos que muestran que “algo pasó”. Entonces, si 20 personas hacen un experimento para ver si leer Finnegans Wake causa locura en humanos, y 19 encuentran que no, ¿cuál pensás que se va a publicar? Obviamente, el único estudio que sí encontró que Finnegans Wake causa locura. Eso es un ejemplo de sesgo de publicación: como nadie publica los 19 estudios que no encontraron efecto, una persona ingenua jamás sabría que existieron. Peor aún, muchos investigadores internalizan este sesgo y terminan autocensurando sus propios trabajos. Como saben que los resultados negativos no van a ser aceptados para su publicación, ni siquiera intentan reportarlos. Como dice una amiga mía: “por cada experimento que lográs publicar, tenés diez fracasos detrás”. Y tiene razón. El problema es que, si bien algunos (quizás la mayoría) de esos estudios fallaron por razones aburridas (por ejemplo, porque cometiste algún error), otros podrían ser verdaderos resultados nulos que deberías reconocer cuando escribís el experimento que sí salió “bien”. Y distinguir entre una cosa y la otra muchas veces es difícil. Un buen punto de partida es un artículo de Ioannidis (2005) con el deprimente título “Por qué la mayoría de los hallazgos publicados son falsos”. También te recomiendo el trabajo de Kühberger, Fritz, y Scherndl (2014), que presenta evidencia estadística de que esto realmente pasa en psicología.

Seguramente hay muchos más temas como este para pensar, pero con esto alcanza para empezar. Lo que realmente quiero señalar es una verdad tan obvia como incómoda: la ciencia del mundo real la hacen personas reales, y solo alguien muy ingenuo puede creer que todos son siempre honestos e imparciales. Los científicos de verdad no suelen ser tan ingenuos, pero por alguna razón el mundo prefiere fingir que lo somos, y los manuales que solemos escribir refuerzan ese estereotipo.

1.13 Resumen

Este capítulo no pretende ofrecer una discusión exhaustiva sobre los métodos de investigación en psicología: para hacerle justicia al tema se necesitaría otro volumen igual de largo que este. Sin embargo, en la vida real, las estadísticas y el diseño de estudios están fuertemente entrelazados, así que es muy útil repasar algunos temas clave. En este capítulo, discutí brevemente los siguientes temas:

• Introducción a la medición psicológica: ¿Qué significa operacionalizar un constructo teórico? ¿Qué significa tener variables y tomar mediciones?

• Escalas de medición y tipos de variables: Recordá que hay dos distinciones diferentes acá: está la diferencia entre datos discretos y continuos, y está la diferencia entre los cuatro tipos de escala (nominal, ordinal, de intervalo y de razón).

• Confiabilidad de una medición: Si mido dos veces lo “mismo”, ¿debería esperar ver el mismo resultado? Solo si mi medición es confiable. Pero, ¿qué significa hablar de hacer lo “mismo”? Bueno, por eso tenemos distintos tipos de confiabilidad. Acordate cuáles son.

• Terminología: predictoras y resultados: ¿Qué rol juegan las variables en un análisis? ¿Te acordás la diferencia entre variables predictoras y variables resultado? ¿Entre dependientes e independientes? Etc.

• Diseños de investigación experimentales y no experimentales: ¿Qué es lo que hace que un experimento sea un experimento? ¿Una bata blanca de laboratorio? ¿O tiene algo que ver con el control que ejerce la persona investigadora sobre las variables?

• Validez y sus amenazas: ¿Tu estudio mide lo que querés que mida? ¿Cómo podrían salir mal las cosas? ¿Y soy yo, o esa fue una lista larguísima de posibles maneras en que las cosas pueden salir mal?

Todo esto debería dejar en claro que el diseño del estudio es una parte crítica de la metodología de investigación. Armé este capítulo a partir del clásico libro de Campbell y Stanley (1963), pero hay una gran cantidad de manuales sobre diseño de investigación. Con solo pasar unos minutos en tu buscador favorito vas a encontrar decenas.

1.14 Videos

1.14.1 Términos en Estadística (video en inglés)

:::

Adair, G. 1984. «The Hawthorne Effect: A Reconsideration of the Methodological Artifact». Journal of Applied Psychology 69: 334-45. https://doi.org/10.1037/0021-9010.69.2.334.

Bickel, P. J., E. A. Hammel, y J. W. O’Connell. 1975. «Sex Bias in Graduate Admissions: Data from Berkeley». Science (New York, N.Y.) 187: 398-404. https://doi.org/10.1126/science.187.4175.398.

Campbell, D. T., y J. C. Stanley. 1963. Experimental and Quasi-Experimental Designs for Research. Boston, MA: Houghton Mifflin.

Evans, J. St. B. T., J. L. Barston, y P. Pollard. 1983. «On the Conflict between Logic and Belief in Syllogistic Reasoning». Memory and Cognition 11: 295-306. https://doi.org/10.3758/BF03196976.

Hothersall, D. 2004. History of Psychology. McGraw-Hill.

Ioannidis, John P. A. 2005. «Why Most Published Research Findings Are False». PLoS medicine 2 (8): 697-701. https://doi.org/10.1371/journal.pmed.0020124.

Kahneman, D., y A. Tversky. 1973. «On the Psychology of Prediction». Psychological Review 80: 237-51. https://doi.org/10.1037/h0034747.

Kühberger, A, A Fritz, y T. Scherndl. 2014. «Publication Bias in Psychology: A Diagnosis Based on the Correlation between Effect Size and Sample Size». Public Library of Science One 9: 1-8.

Pfungst, O. 1911. Clever Hans (The Horse of Mr. von Osten): A Contribution to Experimental Animal and Human Psychology. Traducido por C. L. Rahn. New York: Henry Holt.

Rosenthal, R. 1966. Experimenter Effects in Behavioral Research. New York: Appleton.

Stevens, S. S. 1946. «On the Theory of Scales of Measurement». Science (New York, N.Y.) 103: 677-80. https://doi.org/10.1126/science.103.2684.677.